题目内容
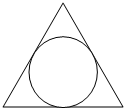如图，正三角形的内切圆半径为1，那么这个正三角形的边长为分析：欲求三角形的边长，已知内切圆半径，可过内心向正三角形的一边作垂线，连接顶点与内切圆心，构造直角三角形求解．
解答：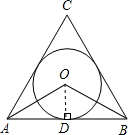
解：过O点作OD⊥AB，则OD=1．
∵O是△ABC的内心，
∴∠OAD=30°；
Rt△OAD中，∠OAD=30°，OD=1，
∴AD=
=
，
∴AB=2AD=2
．
故答案为2
．
解：过O点作OD⊥AB，则OD=1．∵O是△ABC的内心，
∴∠OAD=30°；
Rt△OAD中，∠OAD=30°，OD=1，
∴AD=
| OD |
| tan30° |
| 3 |
∴AB=2AD=2
| 3 |
故答案为2
| 3 |
点评：本题主要考查等边三角形的性质、三角形内切圆的性质，关键在于作辅助线构建直角三角形．
练习册系列答案
高效智能课时作业系列答案
相关题目
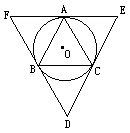
，⊙O的外切正三角形GHK的面积为
．求证
．
，⊙O的外切正三角形GHK的面积为
．求证
．