题目内容
(2009•西城区一模)已知:反比例函数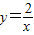 和
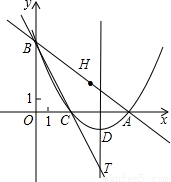
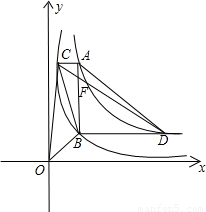
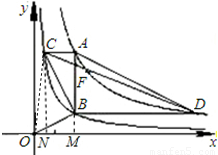
和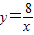 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与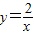 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与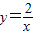 ,
,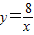 的图象交于点C、D.
的图象交于点C、D.(1)若点A的横坐标为2,求梯形ACBD的对角线的交点F的坐标;
(2)若点A的横坐标为m,比较△OBC与△ABC的面积的大小,并说明理由;
(3)若△ABC与以A、B、D为顶点的三角形相似,请直接写出点A的坐标.
【答案】分析:(1)首先根据点A的横坐标和双曲线的解析式,可以分别求得点A、B、C、D四个点的坐标.根据点C、D的坐标可以运用待定系数法求得直线CD的解析式,根据题意,得点F的横坐标是2,再进一步把x=2代入直线CD的解析式即可求得点F的纵坐标;
(2)根据(1)中的方法可以用m表示出A、B、C、D四个点的坐标,从而求得直角三角形ABC的面积;由于三角形OBC的形状不规则,可以对其面积进行转换.作BM⊥x轴于点M.作CN⊥x轴于点N.根据反比例函数的解析式可知:S△OCN=S△OBM=1.所以该三角形的面积即为梯形CNMB的面积,根据梯形的面积公式进行计算,再进一步比较其大小;
(3)根据两个三角形相似,则夹直角的两组对应边的比应相等,即AB2=AC•BD,再结合(2)中的坐标计算出线段的长度,列方程得m4=16,又m>0,则m=2.
解答:解:(1)如图,由题可知,当点A的横坐标为2时,点A、B、C、D的坐标分别为A(2,4),B(2,1),C( ,4),D(8,1).(1分)
,4),D(8,1).(1分)
解一:直线CD的解析式为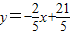 .(2分)
.(2分)
∵AB∥y轴,F为梯形ACBD的对角线的交点,
∴x=2时,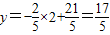 .
.
∴点F的坐标为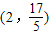 .(3分)
.(3分)
解二: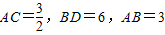 .
.
∵梯形ACBD,AC∥BD,F为梯形ACBD的对角线的交点,
∴△ACF∽△BDF.
∴ .
.
∴ ,
,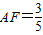 ,点F的纵坐标为
,点F的纵坐标为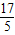 .(2分)
.(2分)
∴点F的坐标为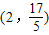 ;(3分)
;(3分)
(2)如图,作BM⊥x轴于点M.作CN⊥x轴于点N.当点A的横坐标为m时,点A、
B、C、D的坐标分别为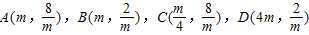 .
.
 .(4分)
.(4分)
S△OBC=S梯形CNMB+S△OCN-S△OBM=S梯形CNMB=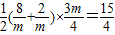 (5分)
(5分)
∴S△OBC>S△ABC;(6分)
(3)点A的坐标为(2,4).(7分)
点评:注意几个结论:(1)双曲线y=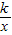 上任意一点向x轴或y轴引垂线,这点、垂足和原点组成的三角形的面积是
上任意一点向x轴或y轴引垂线,这点、垂足和原点组成的三角形的面积是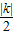 ;(2)平行于x轴的线段的长等于两个点的横坐标差的绝对值;平行于y轴的线段的长等于两个点的纵坐标的差的绝对值.
;(2)平行于x轴的线段的长等于两个点的横坐标差的绝对值;平行于y轴的线段的长等于两个点的纵坐标的差的绝对值.
(2)根据(1)中的方法可以用m表示出A、B、C、D四个点的坐标,从而求得直角三角形ABC的面积;由于三角形OBC的形状不规则,可以对其面积进行转换.作BM⊥x轴于点M.作CN⊥x轴于点N.根据反比例函数的解析式可知:S△OCN=S△OBM=1.所以该三角形的面积即为梯形CNMB的面积,根据梯形的面积公式进行计算,再进一步比较其大小;
(3)根据两个三角形相似,则夹直角的两组对应边的比应相等,即AB2=AC•BD,再结合(2)中的坐标计算出线段的长度,列方程得m4=16,又m>0,则m=2.
解答:解:(1)如图,由题可知,当点A的横坐标为2时,点A、B、C、D的坐标分别为A(2,4),B(2,1),C(
 ,4),D(8,1).(1分)
,4),D(8,1).(1分)解一:直线CD的解析式为
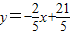 .(2分)
.(2分)∵AB∥y轴,F为梯形ACBD的对角线的交点,
∴x=2时,
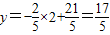 .
.∴点F的坐标为
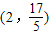 .(3分)
.(3分)解二:
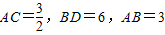 .
.∵梯形ACBD,AC∥BD,F为梯形ACBD的对角线的交点,
∴△ACF∽△BDF.
∴
 .
.∴
 ,
,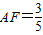 ,点F的纵坐标为
,点F的纵坐标为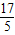 .(2分)
.(2分)∴点F的坐标为
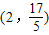 ;(3分)
;(3分)(2)如图,作BM⊥x轴于点M.作CN⊥x轴于点N.当点A的横坐标为m时,点A、
B、C、D的坐标分别为
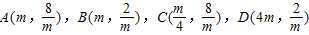 .
. .(4分)
.(4分)S△OBC=S梯形CNMB+S△OCN-S△OBM=S梯形CNMB=
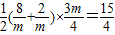 (5分)
(5分)∴S△OBC>S△ABC;(6分)

(3)点A的坐标为(2,4).(7分)
点评:注意几个结论:(1)双曲线y=
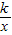 上任意一点向x轴或y轴引垂线,这点、垂足和原点组成的三角形的面积是
上任意一点向x轴或y轴引垂线,这点、垂足和原点组成的三角形的面积是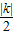 ;(2)平行于x轴的线段的长等于两个点的横坐标差的绝对值;平行于y轴的线段的长等于两个点的纵坐标的差的绝对值.
;(2)平行于x轴的线段的长等于两个点的横坐标差的绝对值;平行于y轴的线段的长等于两个点的纵坐标的差的绝对值. 
练习册系列答案
相关题目
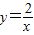 和
和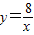 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在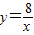 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与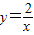 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与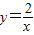 ,
,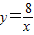 的图象交于点C、D.
的图象交于点C、D.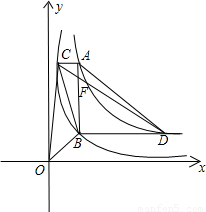
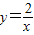 和
和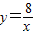 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在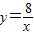 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与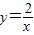 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与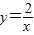 ,
, 的图象交于点C、D.
的图象交于点C、D.
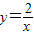 和
和 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在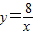 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与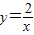 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与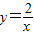 ,
, 的图象交于点C、D.
的图象交于点C、D.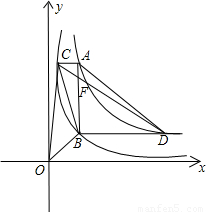
 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.