题目内容
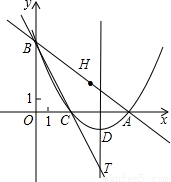
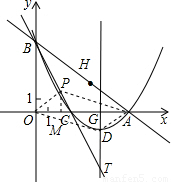
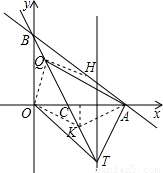
(2009•西城区一模)已知:如图,在平面直角坐标系xOy中,直线 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA-QO|的取值范围.
【答案】分析:(1)点A的坐标是纵坐标为0,得横坐标为8,所以点A的坐标为(8,0);
点B的坐标是横坐标为0,解得纵坐标为6,所以点B的坐标为(0,6);
由题意得:BC是∠ABO的角平分线,所以OC=CH,BH=OB=6
∵AB=10,∴AH=4,
设OC=x,则AC=8-x
由勾股定理得:x=3
∴点C的坐标为(3,0)
将此三点代入二次函数一般式,列的方程组即可求得;
(2)求得直线BC的解析式,根据平行四边形的性质,对角相等,对边平行且相等,借助于三角函数即可求得;
(3)如图,由对称性可知QO=QH,|QA-QO|=|QA-QH|.
当点Q与点B重合时,Q、H、A三点共线,
|QA-QO|取得最大值4(即为AH的长);
设线段OA的垂直平分线与直线BC的交点为K,
当点Q与点K重合时,|QA-QO|取得最小值0.
解答:解:(1)点C的坐标为(3,0).(1分)
∵点A、B的坐标分别为A(8,0),B(0,6),
∴可设过A、B、C三点的抛物线的解析式为y=a(x-3)(x-8).
将x=0,y=6代入抛物线的解析式,
得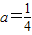 .(2分)
.(2分)
∴过A、B、C三点的抛物线的解析式为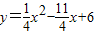 .(3分)
.(3分)
(2)可得抛物线的对称轴为直线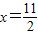 ,顶点D的坐标为
,顶点D的坐标为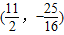 ,
,
设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为y=-2x+6.4分)
设点P的坐标为(x,-2x+6).
解法一:如图,作OP∥AD交直线BC于点P,
连接AP,作PM⊥x轴于点M.
∵OP∥AD,
∴∠POM=∠GAD,tan∠POM=tan∠GAD.
∴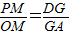 ,
,
即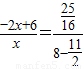 .
.
解得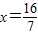 .
.
经检验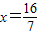 是原方程的解.
是原方程的解.
此时点P的坐标为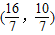 .(5分)
.(5分)
但此时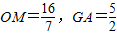 ,OM<GA.
,OM<GA.
∵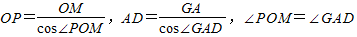 ,
,
∴OP<AD,即四边形的对边OP与AD平行但不相等,
∴直线BC上不存在符合条件的点P(6分)
解法二:如图,取OA的中点E,
作点D关于点E的对称点P,作PN⊥x轴于
点N.则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG.
由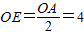 ,可得E点的坐标为(4,0).
,可得E点的坐标为(4,0).
NE=EG= ,ON=OE-NE=
,ON=OE-NE= ,NP=DG=
,NP=DG=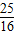 .
.
∴点P的坐标为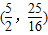 .(5分)
.(5分)
∵x= 时,
时,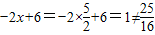 ,
,
∴点P不在直线BC上.
∴直线BC上不存在符合条件的点P.(6分)

(3)|QA-QO|的取值范围是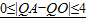 .(8分)
.(8分)
当Q在OA的垂直平分线上与直线BC的交点时,(如点K处),此时OK=AK,则|QA-QO|=0,
当Q在AH的延长线与直线BC交点时,此时|QA-QO|最大,
直线AH的解析式为:y=- x+6,直线BC的解析式为:y=-2x+6,
x+6,直线BC的解析式为:y=-2x+6,
联立可得:交点为(0,6),
∴OQ=6,AQ=10,
∴|QA-QO|=4,
∴|QA-QO|的取值范围是:0≤|QA-QO|≤4.
点评:此题考查了二次函数与一次函数以及平行四边形的综合知识,解题的关键是认真识图,注意数形结合思想的应用.
点B的坐标是横坐标为0,解得纵坐标为6,所以点B的坐标为(0,6);
由题意得:BC是∠ABO的角平分线,所以OC=CH,BH=OB=6
∵AB=10,∴AH=4,
设OC=x,则AC=8-x
由勾股定理得:x=3
∴点C的坐标为(3,0)
将此三点代入二次函数一般式,列的方程组即可求得;
(2)求得直线BC的解析式,根据平行四边形的性质,对角相等,对边平行且相等,借助于三角函数即可求得;
(3)如图,由对称性可知QO=QH,|QA-QO|=|QA-QH|.
当点Q与点B重合时,Q、H、A三点共线,
|QA-QO|取得最大值4(即为AH的长);
设线段OA的垂直平分线与直线BC的交点为K,
当点Q与点K重合时,|QA-QO|取得最小值0.
解答:解:(1)点C的坐标为(3,0).(1分)
∵点A、B的坐标分别为A(8,0),B(0,6),
∴可设过A、B、C三点的抛物线的解析式为y=a(x-3)(x-8).
将x=0,y=6代入抛物线的解析式,
得
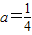 .(2分)
.(2分)∴过A、B、C三点的抛物线的解析式为
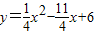 .(3分)
.(3分)(2)可得抛物线的对称轴为直线
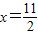 ,顶点D的坐标为
,顶点D的坐标为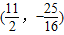 ,
,设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为y=-2x+6.4分)
设点P的坐标为(x,-2x+6).
解法一:如图,作OP∥AD交直线BC于点P,
连接AP,作PM⊥x轴于点M.
∵OP∥AD,
∴∠POM=∠GAD,tan∠POM=tan∠GAD.
∴
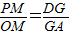 ,
,即
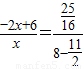 .
.解得
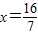 .
.经检验
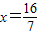 是原方程的解.
是原方程的解.此时点P的坐标为
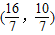 .(5分)
.(5分)但此时
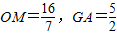 ,OM<GA.
,OM<GA.∵
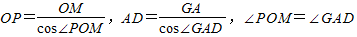 ,
,∴OP<AD,即四边形的对边OP与AD平行但不相等,
∴直线BC上不存在符合条件的点P(6分)

解法二:如图,取OA的中点E,
作点D关于点E的对称点P,作PN⊥x轴于
点N.则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG.
由
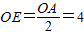 ,可得E点的坐标为(4,0).
,可得E点的坐标为(4,0).NE=EG=
 ,ON=OE-NE=
,ON=OE-NE= ,NP=DG=
,NP=DG=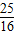 .
.∴点P的坐标为
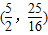 .(5分)
.(5分)∵x=
 时,
时,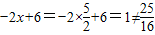 ,
,∴点P不在直线BC上.
∴直线BC上不存在符合条件的点P.(6分)

(3)|QA-QO|的取值范围是
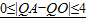 .(8分)
.(8分)当Q在OA的垂直平分线上与直线BC的交点时,(如点K处),此时OK=AK,则|QA-QO|=0,
当Q在AH的延长线与直线BC交点时,此时|QA-QO|最大,
直线AH的解析式为:y=-
 x+6,直线BC的解析式为:y=-2x+6,
x+6,直线BC的解析式为:y=-2x+6,联立可得:交点为(0,6),
∴OQ=6,AQ=10,
∴|QA-QO|=4,
∴|QA-QO|的取值范围是:0≤|QA-QO|≤4.

点评:此题考查了二次函数与一次函数以及平行四边形的综合知识,解题的关键是认真识图,注意数形结合思想的应用.

练习册系列答案
相关题目
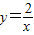 和
和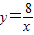 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与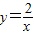 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与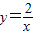 ,
,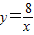 的图象交于点C、D.
的图象交于点C、D.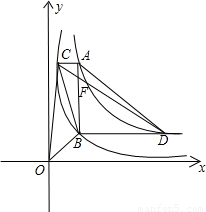
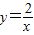 和
和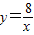 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在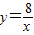 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与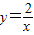 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与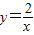 ,
,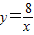 的图象交于点C、D.
的图象交于点C、D.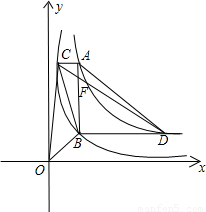
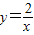 和
和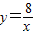 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在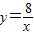 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与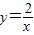 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与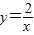 ,
, 的图象交于点C、D.
的图象交于点C、D.
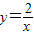 和
和 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在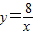 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与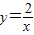 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与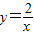 ,
, 的图象交于点C、D.
的图象交于点C、D.