题目内容
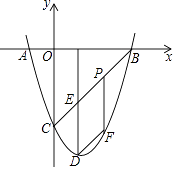
【题目】如图,在平面直角坐标系xOy中,拋物线y=﹣ ![]() x2
x2 ![]() x与x轴交于O,A,点B在抛物线上且横坐标为2.
x与x轴交于O,A,点B在抛物线上且横坐标为2.
(1)如图1,△AOB的面积是多少?
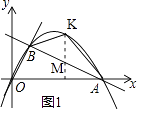
(2)如图1,在线段AB上方的抛物线上有一点K,当△ABK的面积最大时,求点K的坐标及△ABK的面积;
(3)在(2)的条件下,点H 在y轴上运动,点I在x轴上运动.则当四边形BHIK周长最小时,求出H、I的坐标以及四边形BHIK周长的最小值.
【答案】
(1)解:当y=0时,得A(10,0);
当x=2时,y=4,所以B(2,4),
∴ ![]() ;
;
(2)解:过K作KM⊥x轴交AB于M点,
设K(m,﹣ ![]() m2
m2 ![]() m),(2<m<10),
m),(2<m<10),
∵A(10,0),B(2,4),
∴直线AB的解析式为y=﹣ ![]() x+5,
x+5,
则KM=﹣ ![]() m2
m2 ![]() m﹣(﹣
m﹣(﹣ ![]() m+5)=﹣
m+5)=﹣ ![]() m2+3m﹣5,
m2+3m﹣5,
∴S△ABK= ![]() KM|xA﹣xB|=4KM=﹣m2+12m﹣20=﹣(m﹣6)2+16,
KM|xA﹣xB|=4KM=﹣m2+12m﹣20=﹣(m﹣6)2+16,
∴当m=6时,S△ABK有最大值.
此时,K(6,6),S△ABK=16.
(3)解:如图,作点B关于y轴的对称点B′(﹣2,4)、点K关于x轴的对称点K′(6,﹣6),
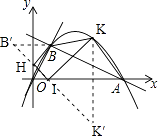
连接B′K′,分别交x轴于点I,交y轴于点H,此时四边形BHIK的周长最小,
∴B′K′的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
∴H(0, ![]() )、I(
)、I( ![]() ,0),
,0),
∴四边形BHIK周长的最小值为B′K′+BK= ![]() +
+ ![]() =2
=2 ![]() +2
+2 ![]() .
.
【解析】(1)要求面积可求高,即yB;(2)(三边均没有水平边或竖直边的三角形可称为斜三角形)△ABK是斜三角形,须过点K做x轴的垂线,把它分割为两个有竖直边的三角形,设出自变量,构建函数,解决最值问题;(3)四边形BHIK周长可转化为多条线段的和,可利用对称法求两线段之和最小,即做出定点B、K分别关于y、x轴的对称点,当三条线段B'H,HI、IK' 在一条直线上时,周长最短..
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案