题目内容
【题目】如图,在矩形ABCD中,AB=8cm,BC=20cm,E是AD的中点.动点P从A点出发,沿A-B-C路线以1cm/秒的速度运动,运动的时间为t秒.将![]() APE以EP为折痕折叠,点A的对应点记为M.
APE以EP为折痕折叠,点A的对应点记为M.
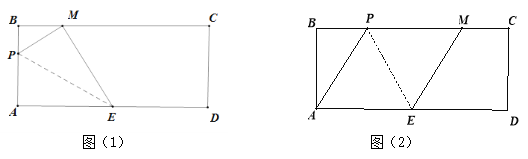
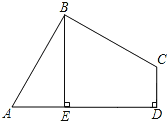
(1) 如图(1),当点P在边AB上,且点M在边BC上时,求运动时间t;
(2) 如图(2),当点P在边BC上,且点M也在边BC上时,求运动时间t;
(3) 直接写出点P在运动过程中线段BM长的最小值 .
【答案】(1)、t=5;(2)、t=14;(3)、2![]() .
.
【解析】
试题分析:(1)、过E作EG⊥BC,根据Rt△BPM的勾股定理求出t的值;(2)、根据Rt△BPA的勾股定理进行求解;(3)、根据函数的性质求出最值.
试题解析:(1)过点E作EG⊥BC于点G,则MG=6,BM=4.PM=PA=t,BP=8-t
在Rt△BPM中,![]() 解得t=5.
解得t=5.
(2) ∵∠APE=∠MPE=∠AEP,∴AP=AE=PM=10,在Rt△BPA中求得,BP=6, ∴t=14.
(3)2![]()

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目