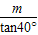题目内容
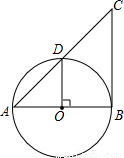
(2008•湖州)如图甲,在等腰直角三角形OAB中,∠OAB=90°,B点在第一象限,A点坐标为(1,0).△OCD与△OAB关于y轴对称.(1)求经过D,O,B三点的抛物线的解析式;
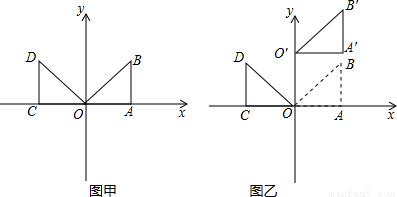
(2)若将△OAB向上平移k(k>0)个单位至△O′A′B(如图乙),则经过D,O,B′三点的抛物线的对称轴在y轴的______.(填“左侧”或“右侧”)
(3)在(2)的条件下,设过D,O,B′三点的抛物线的对称轴为直线x=m.求当k为何值时,|m|=
 .
.
【答案】分析:(1)依题意设所求抛物线的解析式为y=ax2.把点B代入解析式求出抛物线的表达式.
(2)结合图形解答.△OAB≌△OCD,当将其上移,经过D,O,B′三点的抛物线的对称轴显然在y轴左侧
(3)设出抛物线解析式,将D和和B′点坐标代入,得出抛物线系数与k的关系,再由m的取值,求得k.
解答:解:(1)由题意可知:经过D,O,B三点的抛物线的顶点是原点,
故可设所求抛物线的解析式为y=ax2.
∵OA=AB,
∴B点坐标为(1,1).(1分)
∵B(1,1)在抛物线上,
∴1=a×12,a=1,(1分)
∴经过D,O,B三点的抛物线解析式是y=x2.(1分)
(2)把△OAB上移,由图可知经过D,O,B′三点的抛物线的对称轴显然在y轴左侧.(1分)
(3)由题意得:点B′的坐标为(1,1+k),(1分)
因为抛物线过原点,
故可设抛物线解析式为y=a1x2+b1x,
∵抛物线经过点D(-1,1)和点B′(1,1+k),
∴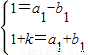 .
.
得a1=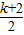 ,b1=
,b1=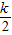 .(2分)
.(2分)
∵抛物线对称轴必在y轴的左侧,
∴m<0,而|m|= ,
,
∴m=- ∴-
∴-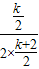 =-
=- ,
,
∴k=4(2分)
即当k=4时,|m|= .(1分)
.(1分)
点评:本题考查的是二次函数的综合运用以及利用待定系数法求出函数解析式,难度中上.
(2)结合图形解答.△OAB≌△OCD,当将其上移,经过D,O,B′三点的抛物线的对称轴显然在y轴左侧
(3)设出抛物线解析式,将D和和B′点坐标代入,得出抛物线系数与k的关系,再由m的取值,求得k.
解答:解:(1)由题意可知:经过D,O,B三点的抛物线的顶点是原点,
故可设所求抛物线的解析式为y=ax2.
∵OA=AB,
∴B点坐标为(1,1).(1分)
∵B(1,1)在抛物线上,
∴1=a×12,a=1,(1分)
∴经过D,O,B三点的抛物线解析式是y=x2.(1分)
(2)把△OAB上移,由图可知经过D,O,B′三点的抛物线的对称轴显然在y轴左侧.(1分)
(3)由题意得:点B′的坐标为(1,1+k),(1分)
因为抛物线过原点,
故可设抛物线解析式为y=a1x2+b1x,
∵抛物线经过点D(-1,1)和点B′(1,1+k),
∴
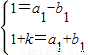 .
.得a1=
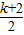 ,b1=
,b1=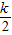 .(2分)
.(2分)∵抛物线对称轴必在y轴的左侧,
∴m<0,而|m|=
 ,
,∴m=-
 ∴-
∴-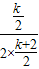 =-
=- ,
,∴k=4(2分)
即当k=4时,|m|=
 .(1分)
.(1分)点评:本题考查的是二次函数的综合运用以及利用待定系数法求出函数解析式,难度中上.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 .
.