题目内容
如图1,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,点
上运动,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且使得四边形
上,且使得四边形![]() 是矩形.设
是矩形.设![]() 的长为
的长为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,已知
,已知![]() 是
是![]() 的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示).
的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示).
(1)求![]() 的长;
的长;
(2)当![]() 为何值时,矩形
为何值时,矩形![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.
为了解决这个问题,孔明和研究性学习小组的同学作了如下讨论:
张明:图2中的抛物线过点(12,36)在图1中表示什么呢?
李明:因为抛物线上的点![]() 是表示图1中
是表示图1中![]() 的长与矩形
的长与矩形![]() 面积的对应关系,那么,(12,36)表示当
面积的对应关系,那么,(12,36)表示当![]() 时,
时,![]() 的长与矩形
的长与矩形![]() 面积的对应关系.
面积的对应关系.
赵明:对,我知道纵坐标36是什么意思了!
孔明:哦,这样就可以算出![]() ,这个问题就可以解决了.
,这个问题就可以解决了.
请根据上述对话,帮他们解答这个问题.

 |
图1 图2
(1)当![]() 时,
时,![]() ∴
∴![]() ,
,
又在![]() 中,
中,![]() ,∴
,∴![]() ∴
∴![]() ∴
∴![]()
(2)解法一:若 ![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() ,整理得
,整理得![]()
∴ 当![]() 时,
时,![]() .
.
解法二:由![]() ,结合图象可知抛物线经过点(0,0)、(16,0)、(12,36),可设抛物线解析式为
,结合图象可知抛物线经过点(0,0)、(16,0)、(12,36),可设抛物线解析式为![]() ,将(12,36)代入求得
,将(12,36)代入求得![]() ,∴
,∴![]() ,整理得
,整理得![]() ,∴ 当
,∴ 当![]() 时,
时,![]() .
.
解法三:由![]() ,结合图象可知抛物线经过点(0,0)、(16,0),知抛物线对称轴为
,结合图象可知抛物线经过点(0,0)、(16,0),知抛物线对称轴为![]() ,∴抛物线顶点的横坐标为8.∴当
,∴抛物线顶点的横坐标为8.∴当![]() 时,矩形
时,矩形![]() 的面积最大,此时,
的面积最大,此时,![]() ,∴
,∴![]() ,∴最大面积为48.
,∴最大面积为48.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目

 分)
分) 中,
中, ∥
∥ ,
, ,点
,点 在边
在边 上,
上, 与
与 相交于点
相交于点 ,且
,且 .
.
 ∽
∽ ; (6分)
; (6分) . (6分)
. (6分) 分)
分)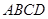 中,
中,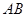 ∥
∥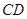 ,
, ,点
,点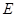 在边
在边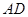 上,
上,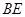 与
与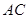 相交于点
相交于点 ,且
,且 .
.
 ∽
∽ ; (6分)
; (6分) . (6分)
. (6分) 中,
中, ∥
∥ ,
, ,点
,点 在边
在边 上,
上, 与
与 相交于点
相交于点 ,且
,且 .
.
 ∽
∽ ; (6分)
; (6分) . (6分)
. (6分)