题目内容
已知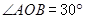 ,点
,点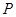 在
在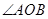 的内部,
的内部,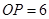 ,
,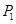 与
与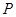 关于
关于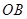 对称,
对称,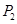 与
与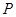 关于
关于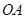 对称,则△
对称,则△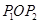 的周长为 ;若
的周长为 ;若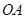 上有一动点
上有一动点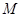 ,
,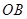 上有一动点
上有一动点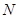 ,则△
,则△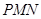 的最小周长为 .
的最小周长为 .
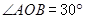 ,点
,点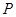 在
在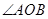 的内部,
的内部,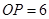 ,
,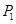 与
与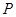 关于
关于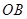 对称,
对称,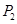 与
与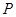 关于
关于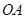 对称,则△
对称,则△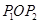 的周长为 ;若
的周长为 ;若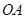 上有一动点
上有一动点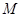 ,
,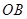 上有一动点
上有一动点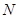 ,则△
,则△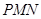 的最小周长为 .
的最小周长为 .18,6
(1)∵P为∠AOB内部一点,点P关于OA、OB的对称点分别为P1、P2,
∴OP=OP1=OP2=6,且∠P1OP2=2∠AOB=60°,
∴故△OP1P2是等边三角形.
∴△P1OP2的周长=3×6=18;
(2)分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=6,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=6.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=6.
∴OP=OP1=OP2=6,且∠P1OP2=2∠AOB=60°,
∴故△OP1P2是等边三角形.
∴△P1OP2的周长=3×6=18;
(2)分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=6,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=6.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=6.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 中,A(1,2),B(3,1),C(-2,-1).
中,A(1,2),B(3,1),C(-2,-1).
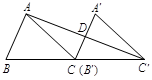
 关于
关于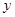 轴的对称图形
轴的对称图形 .
.  的坐标(直接写答案).
的坐标(直接写答案).
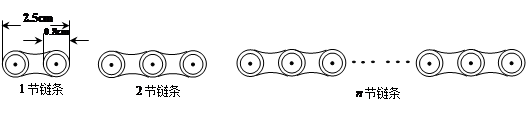
 关于原点中心对称的点的坐标是( )
关于原点中心对称的点的坐标是( ) .(-1,-3);
.(-1,-3);  .(1,-3);
.(1,-3);  .(1,3);
.(1,3);  .(3,-1).
.(3,-1).
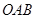 绕点
绕点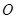 逆时针旋转80°得到△
逆时针旋转80°得到△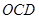 ,若∠
,若∠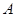 =
=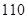 °,∠
°,∠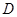 =
=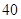 °,则∠
°,则∠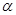 的度数是
的度数是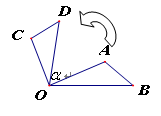
 °
°
 °
°