Question

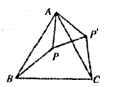
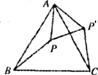
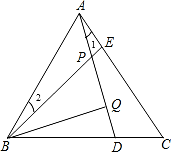
如下图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD与Q，PQ=4，PE=1。
（1）求证∠BPQ=60°；
（2）求AD的长。

Answer 1

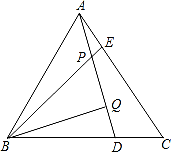
解：（1）∵△ABC是等边三角形，
∴AB=AC，∠BAE=∠ACD=60°，
又∵AE=CD，
∴△BAE≌△ACD，
∴∠1=∠2，
∵∠BAE=∠1+∠BAD=60°，
∴∠BAE=∠2+∠BAD=60°，
∴∠BPQ=60°；
（2）∵BQ⊥AD，
∴∠BQP=90°，
又∵∠BPQ=60°，
∴∠PBQ=30°，
∴BP=2PQ=2×4=8，
∴BE=BP+PE=8+1=9，
由（1）知△BAE≌△ACD，
∴CD=AE=9。