Question

【题目】已知：如图，等边三角形ABD与等边三角形ACE具有公共顶点A，连接CD，BE，交于点P.

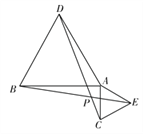
（1）观察度量， 的度数为＿＿＿＿.（直接写出结果）

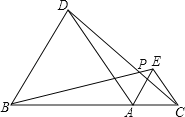
（2）若绕点A将△ACE旋转，使得，请你画出变化后的图形.（示意图）

（3）在（2）的条件下，求出的度数.

Answer 1

【答案】（1）120°;（2）作图见解析；（3）∠BPC =120°．

【解析】分析：（1）∠BPC的度数为120°，理由为：由△ABD与△ACE都是等边三角形，利用等边三角形的性质得到∠DAB=∠ABD=∠CAE=60°，AD=AB，AC=AE，利用等式的性质得到夹角相等，利用SAS得出三角形DAC与三角形BAE全等，由全等三角形的对应角相等得到∠ADC=∠ABE，利用外角性质，等量代换即可得到所求；（2）作出相应的图形，如图所示；（3）解法同（1），求出∠BPC的度数即可．

本题解析：

（1）∠BPC的度数为120°，理由为：

证明：∵△ABD与△ACE都是等边三角形，

∴∠DAB=∠ABD=∠CAE=60°，AD=AB，AC=AE，

∴∠DAB+∠BAC=∠CAE+∠BAC，即∠DAC=∠BAE，

在△DAC与△BAE中，

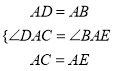，∴△DAC≌△BAE（SAS），

∴∠ADC=∠ABE，∵∠ADC+∠CDB=60°，∴∠ABE+∠CDB=60°，

∴∠BPC=∠DBP+∠PDB=∠ABE+∠CDB+∠ABC=120°；

（2）作出相应的图形，如图所示；

（3）∵△ABD与△ACE都是等边三角形，

∴∠ADB=∠BAD=∠ABD=∠CAE=60°，AD=AB，AC=AE，

∴∠DAB+∠DAE=∠CAE+∠DAE，即∠DAC=∠BAE，

在△DAC与△BAE中，

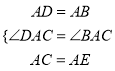，∴△DAC≌△BAE（SAS），∴∠ADC=∠ABE，∵∠ABE+∠DBP=60°，

∴∠ADC+∠DBP=60°，∴∠BPC=∠BDP+∠PBD=∠ADC+∠DBP+∠ADB=120°．