题目内容
课题学习时，老师布置画一个三角形ABC，使∠A=30°，AB=10cm，∠A的对边BC可以在长为4cm、5cm、6cm、11cm四条线段中任选，这样最多可以画（ ）个互不全等的三角形．
| A、3个 | B、4个 | C、5个 | D、6个 |
分析：如图，过B作BD⊥直线AC于D，则线段BD的长度是B到直线AC的最短距离，而利用∠A=30°，AB=10cm可以求出BD，利用垂线段最短即可求解．
解答：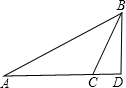
解：如图，过B作BD⊥直线AC于D，
则线段BD的长度是B到直线AC的最短距离，
∵∠A=30°，AB=10cm，
∴BD=
AB=5cm，而垂线段最短，
∴在长为4cm、5cm、6cm、11cm四条线段中有5cm、11cm可以各画1个互不全等的三角形，6cm可以画二个互不全等的三角形．
故选B．
解：如图，过B作BD⊥直线AC于D，则线段BD的长度是B到直线AC的最短距离，
∵∠A=30°，AB=10cm，
∴BD=
| 1 |
| 2 |
∴在长为4cm、5cm、6cm、11cm四条线段中有5cm、11cm可以各画1个互不全等的三角形，6cm可以画二个互不全等的三角形．
故选B．
点评：此题从边的方面考查三角形，涉及分类讨论的思想方法．判断三角形是否成立利用垂线段最短这个距离．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目