题目内容
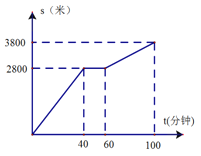
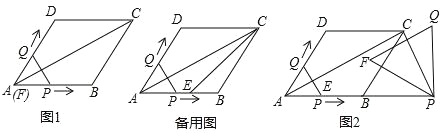
【题目】已知：如图1，菱形ABCD的边长为6，∠DAB=60°，点E是AB的中点，连接AC、EC．点Q从点A出发，沿折线A﹣D﹣C运动，同时点P从点A出发，沿射线AB运动，P、Q的速度均为每秒1个单位长度；以PQ为边在PQ的左侧作等边△PQF，△PQF与△AEC重叠部分的面积为S，当点Q运动到点C时P、Q同时停止运动，设运动的时间为t．
（1）当等边△PQF的边PQ恰好经过点D时，求运动时间t的值；当等边△PQF的边QF 恰好经过点E时，求运动时间t的值；
（2）在整个运动过程中，请求出S与t之间的函数关系式和相应的自变量t的取值范围；
（3）如图2，当点Q到达C点时，将等边△PQF绕点P旋转α°（0＜α＜360），直线PF分别与直线AC、直线CD交于点M、N．是否存在这样的α，使△CMN为等腰三角形？若存在，请直接写出此时线段CM的长度；若不存在，请说明理由．
【答案】（1)9（秒）；(2)0＜t≤3时，S=
PG×AG=
；当3＜t≤6时，S=
，
当6＜t≤9时，如图5，S=
；当9＜t≤12时，S=
；
（3）①α=150°如图7，CM=2
；②α=105°，如图8，CM=12-6；③α=60°，如图9，CM=6；④α=15°，如图10，CM=12+6．
【解析】
试题分析：（1）根据题意求出运动的距离，再除以速度即可求出时间；
（2）分当0＜t≤3时，当3＜t≤6时，当6＜t≤9时，当9＜t≤12时，四种情况，分别求出重叠部分面积即可；
（3）分交点都在BC左侧，顶角为120°，交点都在BC右侧时，顶角可能为30°和120°；交点在BC两侧时，顶角为150°进行讨论求解即可．
试题解析：（1）当等边△PQF的边PQ恰好经过点D时，
如图1
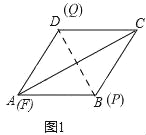
AQ=AD=6，∴t=6÷1=6（秒）；当等边△PQF的边QF 恰好经过点E时，
如图2
由菱形ABCD的边长为6，∠DAB=60°，P、Q的速度均为每秒1个单位长度，
知：∠APQ=60°，∠QEB=60°，∴QE∥AD，∵点E是AB的中点，
∴此时点Q是CD的中点，可求：AD+DQ=6+3=9，所以t=9÷1=9（秒）；
（2）
如图3
当0＜t≤3时，由菱形ABCD的边长为6，∠DAB=60°，可求：∠PAG=30°，
∵∠APQ=60°，∴∠AGP=90°，由AP=t，可求：PG=
t，AG=
t，
∴S=PG×AG=
；
当3＜t≤6时，
如图4
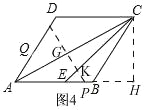
AE=3，AP=t，∴PE=t﹣3，过点C作AB的垂线，垂足为H，
由菱形ABCD的边长为6，∠DAB=60°，可求：CH=3
，BH=3，EH=6，
tan∠KEB=
，过点K作KM⊥AB，可求KM=
，
∴S△PEK=
，可求∠QAG=30°，又∠AQG=60°，AQ=t，
可求∠AGQ=90°，DG=
t，GQ=t，∴S△AGQ=
，等边三角形APD的面积为：
∴S=
﹣
﹣
=
，
当6＜t≤9时，如图5
与前同理可求：S△FQP=
，S△GQN=
，S△KEP=
，
∴S=
﹣
﹣=
，
当9＜t≤12时，
如图6
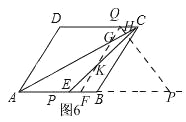
求出：S△PQF=，S△QGH=
；S△NEP=；S△KEF=
，
∴S=S△PQF﹣S△QGH﹣S△NEP+S△KEF=﹣
﹣+
=
；
（3）
逆时针旋转：
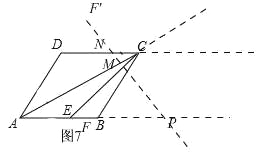
①α=150°，如图7此时，易求∠CNM=∠NCM=∠APM=∠MAP=∠DAP=30°，
可证△ACD∽△APM，∴
，
易求AP=12，AC=6，AD=6，解得：AM=4，所以，CM=2；
②α=105°，如图8
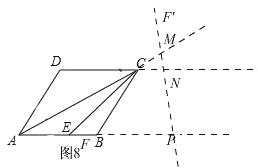
此时，易求CM=CN，∠CMN=∠CNM=∠APM=75°，∴AM=AP=12，
在菱形ABCD中，AD=CD=6，∠D=120°，
可求AC=6，所以，CM=12-6；
③α=60°，如图9
此时，易求∠CMN=∠MCN=∠ACB=30°，∴BC∥PM，由AB=BP=6可得，CM=AC=6
所以：CM=6；
④α=15°，如图10
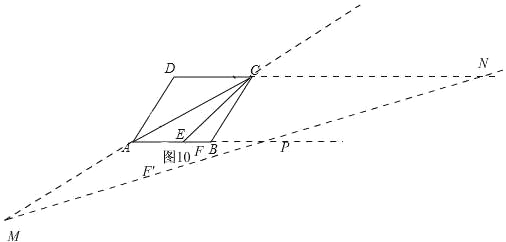
此时，易求∠APM=∠M=15°，∴AM=AP=12，所以：CM=AM+AC，CM=12+6．
