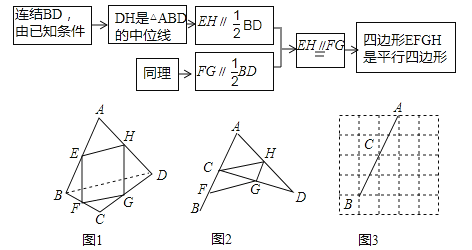
��Ŀ����
����Ŀ����ͼ����֪��ABC�У���B=��C��AB=AC=12cm��BC=8cm����DΪAB���е㣮�����P���߶�BC����2cm/s���ٶ���B����C���˶���ͬʱ����Q���߶�CA���ɵ�C��A���˶��� 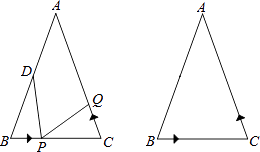
��1������Q���˶��ٶ����P���˶��ٶ���ȣ�����1���BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��2������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
���𰸡�
��1���⣺��BPD�ա�CPQ��
�������¡�t=1s��
��BP=CQ=2��1=2cm��
��AB=12cm����DΪAB���е㣬
��BD=6cm��
�֡�PC=BC��BP��BC=8cm��
��PC=8��2=6cm��
��PC=BD��
�֡�AB=AC��
���B=��C��
�ڡ�BPD�͡�CPQ�У�

���BPD�ա�CQP
��2���⣺�ߵ�Q���˶��ٶ����P���˶��ٶȲ���ȣ�
��BP��CQ��
�֡ߡ�BPD���CPQȫ�ȣ���B=��C��
��BP=PC=4cm��CQ=BD=6cm��
���P����Q�˶���ʱ��Ϊ4��2=2s��
��Q����˶��ٶ�Ϊ6��2=3��cm/s��
����������1����BPD�ա�CPQ��������֪�������BP=CQ��PC=BD������SAS֤����BPD�ա�CQP����2���ɵ�Q���˶��ٶ����P���˶��ٶȲ���ȣ�����BP��CQ�����ɡ�BPD���CPQȫ�ȣ���B=��C���õ�BP=PC=4cm��CQ=BD=6cm���Ӷ������P����Q�˶���ʱ��Ϊ4��2=2�룬���ɽ��

 ��У����ϵ�д�
��У����ϵ�д�