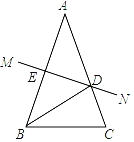
题目内容
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )

A. 5对 B. 6对 C. 7对 D. 8对
【答案】C
【解析】
题中相等的角有:∠ABC=∠ACB、∠ADB=∠AEC=90°、∠BOE=∠COD、∠EAC=∠DAB,根据这些相等角可得出的相似三角形有:
△ADB∽△AEC(∠A=∠A,∠ADB=∠AEC);
△BEC∽△CDB(∠BEC=∠CDB,∠ABC=∠ACB);
△BOE∽△COD(∠BEC=∠CDB,∠BOE=∠COD);
△COD∽△CAE(∠ACE=∠OCD,∠CDO=∠CEA);
同理可证得:△BOE∽△BAD、△BOE∽△CAE、△COD∽△BAD;
∵在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高;
∴∠ABC=∠ACB,∠BEC=∠CDB=90°
∴△BEC∽△CDB
∵∠EOB=∠DOC,∠BEC=∠CDB=90°
∴△BEO∽△CDO
∵∠ABD=∠ABD,∠BEO=∠BDA=90°
∴△BEO∽△BDA
同理△CDO∽△CEA;
∵∠A=∠A,∠AEC=∠ADB=90°
∴△AEC∽△ADB
∴共有7对相似三角形.
故选C.

【题目】在抗洪抢险救灾中,某地粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到没有受洪水威胁的A,B两仓库,已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为60吨,B库的容量为120吨,从甲、乙两库到A、B两库的路程和运费如表(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
若从甲库运往A库粮食x吨,
(Ⅰ)填空(用含x的代数式表示):
①从甲库运往B库粮食 吨;
②从乙库运往A库粮食 吨;
③从乙库运往B库粮食 吨;
(Ⅱ)写出将甲、乙两库粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式,并求出当从甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?