Question

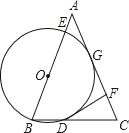
【题目】如图所示，P是⊙O外一点，PA，PB分别和⊙O切于A，B两点，C是上任意一点，过C作⊙O的切线分别交PA，PB于D，E．(1)若△PDE的周长为10，则PA的长为___ __，(2)连结CA、CB，若∠P=50°，则∠BCA的度数为___ __度.

Answer 1

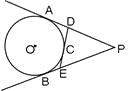
【答案】5，115

【解析】

（1）由于PA、PB、DE都是⊙O的切线，可根据切线长定理将△PDE的周长转化为切线PA、PB的长．

（2）根据切线长定理即可证得△PEF 周长等于2PA即可求解；根据切线的性质以及四边形的内角和定理即可求得∠AOB的度数，然后根据∠EOF=∠AOB即可求出∠BCA的度数．

解：（1）∵PA、PB、DE分别切⊙O于A、B、C，

∴PA=PB，DA=DC，EC=EB；

∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10；

∴PA=PB=5；

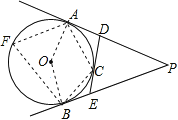
（2）连接OA、OB、AC、BC，在⊙O上取一点F，连接AF、BF，

∵PA、PB分别切⊙O 于A、B；

∴∠PAO=∠PRO=90°

∴∠AOB=360°-90°-90°-50°=130°；

∴∠AFB=∠AOB=65°，

∵∠AFB+∠BCA=180°

∴∠BCA=180°-65°=115°；

故答案是：5，115°．