题目内容
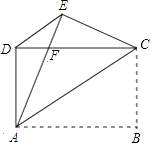
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是上半圆的弦,过点
是上半圆的弦,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作切线
作切线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且与
,且与![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() 的度数分别是
的度数分别是![]() .
.
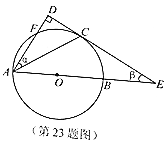
(1)用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
(2)连接![]() 与
与![]() 交于点
交于点![]() ,当点
,当点![]() 是
是![]() 的中点时,求
的中点时,求![]() ,
,![]() 的值.
的值.
【答案】(1)β=90°-2α(0°<α<45°);(2)α=β=30°.
【解析】
试题分析:(1)首先证明∠DAE=2α,在Rt△ADE中,根据两锐角互余,可知2α+β=90°,(0°<α<45°);
(2)连接OF交AC于O′,连接CF.只要证明四边形AFCO是菱形,推出△AFO是等边三角形即可解决问题;
试题解析:(1)连接OC.
∵DE是⊙O的切线,∴OC⊥DE,
∵AD⊥DE,∴AD∥OC,∴∠DAC=∠ACO,
∵OA=OC,∴∠OCA=∠OAC,∴∠DAE=2α,
∵∠D=90°,∴∠DAE+∠E=90°,
∴2α+β=90°(0°<α<45°),即β=90°-2α(0°<α<45°).
(2)连接OF交AC于O′,连接CF.
∵AO′=CO′,∴AC⊥OF,∴FA=FC,∴∠FAC=∠FCA=∠CAO,
∴CF∥OA,∵AF∥OC,∴四边形AFCO是平行四边形,
∵OA=OC,∴四边形AFCO是菱形,∴AF=AO=OF,
∴△AOF是等边三角形,∴∠FAO=2α=60°,∴α=30°,
∵2α+β=90°,∴β=30°,∴α=β=30°.

 名校课堂系列答案
名校课堂系列答案【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.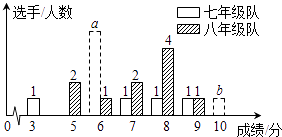
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.