题目内容
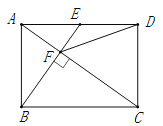
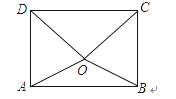
【题目】如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长________
【答案】2![]() d
d
【解析】∵OD=OC,∴O在CD的垂直平分线线上,∠ODC=∠OCD,
∵四边形ABCD是矩形,∴AD=BC,∠ABC=∠ADC=∠BCD=90°,
∴∠ADC﹣∠ODC=∠BCD﹣∠OCD,
即∠ADO=∠BCO,
在△ADO和△BCO中, 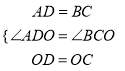 ,
,
∴△ADO≌△BCO(SAS),
∴OA=OB,
∴O在AB的垂直平分线上,
过O作MN⊥AB与N交CD于M,如图所示:
则AN=BN,NM⊥CD,OM=3d,ON=d,
∴BC=MN=3d+d=4d,BN=![]() =
= ![]() ,
,
∴AB=AN+BN=2![]() d,
d,
∴AC=![]() =2
=2![]() d,
d,
故答案为:2![]() d.
d.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目