题目内容
 如图,已知抛物线
如图,已知抛物线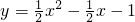 与x轴相交于点A、B,与y轴相交于C.
与x轴相交于点A、B,与y轴相交于C.
(1)求点A、B、C的坐标及直线BC的解析式;
(2)设抛物线的顶点为点D,求△ACD的面积S
(3)在直线BC上是否存在一点P,使△ACP是以AC为一腰的等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
解:(1)把y=0代入抛物线得: x2-
x2- x-1=0,
x-1=0,
解得:x1=2,x2=-1,
∴A(2,0),B(-1,0),
把x=0代入抛物线得:y=0-0-1=-1,
∴C(0,-1),
设直线BC的解析式是y=kx+b,
把B(-1,0),C(0,-1)代入得: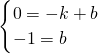 ,
,
解得:k=-1,b=-1,
∴y=-x-1,
答:A(2,0),B(-1,0),C(0,-1),直线BC的解析式是y=-x-1.
(2) 过D作DN⊥OA于N,
过D作DN⊥OA于N,
∵y= x2-
x2- x-1,
x-1,
∴x=- =-
=-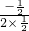 =
= ,
,
把x= 代入抛物线得:y=-
代入抛物线得:y=- ,
,
∴D( ,-
,- ),
),
∴N( ,0),
,0),
∵A(2,0),C(0,-1),
∴AN=2- =
= ,ON=
,ON= ,DN=
,DN= ,OC=1,
,OC=1,
∴S△ACD=St梯形ONDC+S△AND-S△AND,
= ×(1+
×(1+ )×
)× +
+ ×
× ×
× -
- ×2×1,
×2×1,
= ,
,
答:△ACD的面积是 .
.
(3)分为两种情况:
①以C为圆心,以AC为半径画弧,交BC于P、P′,
此时所得三角形ACP和三角形ACP′是等腰三角形,
设此时点的坐标是(x,-x-1),
∵A(2,0),C(0,-1),AC=CP,
由勾股定理得:AC2=CP′2,
∴12+22=(0-x)2+[-1-(-x-1)]2,
解得:x=±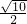 ,
,
当x=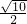 时,-x-1=-
时,-x-1=-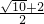 ,
,
当x=-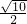 时,-x-1=
时,-x-1= ,
,
∴P的坐标是(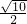 ,-
,-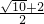 )或(-
)或(-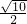 ,
, ),
),
②以A为圆心,以AC为半径画弧,交BC于P″,
同法可得到:12+22=(2-x)2+[0-(-x-1)]2,
解得:x1=0,x2=1,
∵C(0,-1),
∴x=0舍去,
∴x=1,-x-1=-2,
∴P″(1,-2).
答:在直线BC上存在一点P,使△ACP是以AC为一腰的等腰三角形,点P的坐标是(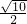 ,-
,-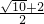 )或(-
)或(-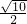 ,
, )或(1,-2).
)或(1,-2).
分析:(1)分别把x=0和y=0代入抛物线,即可求出A、B、C的坐标,设直线BC的解析式是y=kx+b,把B、C的坐标代入求出即可;
(2)求出抛物线的顶点坐标,过D作DN⊥OA于N,根据S△ACD=St梯形ONDC+S△AND-S△AND和三角形的面积代入求出即可;
(3)分为两种情况:①以C为圆心,以AC为半径画弧,交BC于P、P′,设此时点的坐标是(x,-x-1),根据勾股定理得出12+22=(0-x)2+[-1-(-x-1)]2,即可求出此时P的坐标;②以A为圆心,以AC为半径画弧,交BC于P″,同法可得到12+22=(2-x)2+[0-(-x-1)]2,求出即可.
点评:本题综合考查了等腰三角形的判定,三角形的面积,用待定系数法求出一次函数的解析式,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,题目比较好,但是有一定的难度,对学生提出较高的要求,分类讨论思想的运用.
 x2-
x2- x-1=0,
x-1=0,解得:x1=2,x2=-1,
∴A(2,0),B(-1,0),
把x=0代入抛物线得:y=0-0-1=-1,
∴C(0,-1),
设直线BC的解析式是y=kx+b,
把B(-1,0),C(0,-1)代入得:
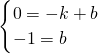 ,
,解得:k=-1,b=-1,
∴y=-x-1,
答:A(2,0),B(-1,0),C(0,-1),直线BC的解析式是y=-x-1.
(2)
 过D作DN⊥OA于N,
过D作DN⊥OA于N,∵y=
 x2-
x2- x-1,
x-1,∴x=-
 =-
=-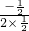 =
= ,
,把x=
 代入抛物线得:y=-
代入抛物线得:y=- ,
,∴D(
 ,-
,- ),
),∴N(
 ,0),
,0),∵A(2,0),C(0,-1),
∴AN=2-
 =
= ,ON=
,ON= ,DN=
,DN= ,OC=1,
,OC=1,∴S△ACD=St梯形ONDC+S△AND-S△AND,
=
 ×(1+
×(1+ )×
)× +
+ ×
× ×
× -
- ×2×1,
×2×1,=
 ,
,答:△ACD的面积是
 .
.(3)分为两种情况:

①以C为圆心,以AC为半径画弧,交BC于P、P′,
此时所得三角形ACP和三角形ACP′是等腰三角形,
设此时点的坐标是(x,-x-1),
∵A(2,0),C(0,-1),AC=CP,
由勾股定理得:AC2=CP′2,
∴12+22=(0-x)2+[-1-(-x-1)]2,
解得:x=±
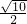 ,
,当x=
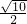 时,-x-1=-
时,-x-1=-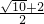 ,
,当x=-
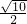 时,-x-1=
时,-x-1= ,
,∴P的坐标是(
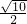 ,-
,-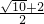 )或(-
)或(-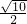 ,
, ),
),②以A为圆心,以AC为半径画弧,交BC于P″,
同法可得到:12+22=(2-x)2+[0-(-x-1)]2,
解得:x1=0,x2=1,
∵C(0,-1),
∴x=0舍去,
∴x=1,-x-1=-2,
∴P″(1,-2).
答:在直线BC上存在一点P,使△ACP是以AC为一腰的等腰三角形,点P的坐标是(
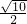 ,-
,-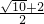 )或(-
)或(-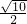 ,
, )或(1,-2).
)或(1,-2).分析:(1)分别把x=0和y=0代入抛物线,即可求出A、B、C的坐标,设直线BC的解析式是y=kx+b,把B、C的坐标代入求出即可;
(2)求出抛物线的顶点坐标,过D作DN⊥OA于N,根据S△ACD=St梯形ONDC+S△AND-S△AND和三角形的面积代入求出即可;
(3)分为两种情况:①以C为圆心,以AC为半径画弧,交BC于P、P′,设此时点的坐标是(x,-x-1),根据勾股定理得出12+22=(0-x)2+[-1-(-x-1)]2,即可求出此时P的坐标;②以A为圆心,以AC为半径画弧,交BC于P″,同法可得到12+22=(2-x)2+[0-(-x-1)]2,求出即可.
点评:本题综合考查了等腰三角形的判定,三角形的面积,用待定系数法求出一次函数的解析式,勾股定理等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,题目比较好,但是有一定的难度,对学生提出较高的要求,分类讨论思想的运用.

练习册系列答案
相关题目
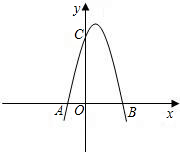 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).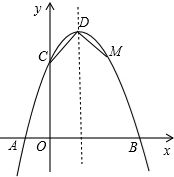 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1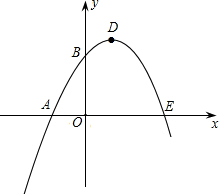 函数的最大值是4.
函数的最大值是4.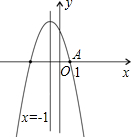 (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( ) 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).