题目内容
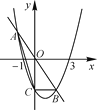
【题目】已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为![]() ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)当原点O为线段AB的中点时,k的值为﹣2,点A的坐标为(﹣![]() ,2
,2![]() ),点B的坐标为(
),点B的坐标为(![]() ,﹣2
,﹣2![]() ).(3)不存在,理由详见解析.
).(3)不存在,理由详见解析.
【解析】试题分析:(1)令x=0求出y值即可得出C点的坐标,又有点(﹣1,0)、(3,0),利用待定系数法求抛物线的解析式即可;(2)将正比例函数解析式代入抛物线解析式中,找出关于x的一元二次方程,根据根与系数的关系即可得出“xA+xB=2+k,xAxB=﹣3”,结合点O为线段AB的中点即可得出xA+xB=2+k=0,由此得出k的值,将k的值代入一元二次方程中求出xA、xB,在代入一次函数解析式中即可得出点A、B的坐标;(3)假设存在,利用三角形的面积公式以及(2)中得到的“xA+xB=2+k,xAxB=﹣3”,即可得出关于k的一元二次方程,结合方程无解即可得出假设不成立,从而得出不存在满足题意的k值.
试题解析:(1)令抛物线y=ax2+bx﹣3中x=0,则y=﹣3,
∴点C的坐标为(0,﹣3).
∵抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,
∴有![]() ,解得:
,解得:![]() ,
,
∴此抛物线的解析式为y=x2﹣2x﹣3.
(2)将y=kx代入y=x2﹣2x﹣3中得:kx=x2﹣2x﹣3,
整理得:x2﹣(2+k)x﹣3=0,
∴xA+xB=2+k,xAxB=﹣3.
∵原点O为线段AB的中点,
∴xA+xB=2+k=0,
解得:k=﹣2.
当k=﹣2时,x2﹣(2+k)x﹣3=x2﹣3=0,
解得:xA=﹣![]() ,xB=
,xB=![]() .
.
∴yA=﹣2xA=2![]() ,yB=﹣2xB=2
,yB=﹣2xB=2![]() .
.
故当原点O为线段AB的中点时,k的值为﹣2,点A的坐标为(﹣![]() ,2
,2![]() ),点B的坐标为(
),点B的坐标为(![]() ,﹣2
,﹣2![]() ).
).
(3
由(2)可知:xA+xB=2+k,xAxB=﹣3,
S△ABC=![]() OC|xA﹣xB|=
OC|xA﹣xB|=![]() ×3×
×3×![]() =
=![]() ,
,
∴(2+k)2﹣4×(﹣3)=10,即(2+k)2+2=0.
∵(2+k)2非负,无解.
故假设不成立.
所以不存在实数k使得△ABC的面积为![]() .
.

【题目】“六一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )

转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
A. 当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
B. 假如你去转动转盘一次,获得铅笔的概率大约是0.70
C. 如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D. 转动转盘10次,一定有3次获得文具盒