题目内容
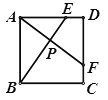
【题目】如图,E、F分别是正方形ABCD的边AD、CD上的点,且AE=DF,AF、BE相交于点P,设AB=![]() ,AE=
,AE=![]()
![]() ,则下列结论:①△ABE≌△DAF;②AF⊥BE;③
,则下列结论:①△ABE≌△DAF;②AF⊥BE;③![]() ;④若
;④若![]() ,连接BF,则tan∠EBF=
,连接BF,则tan∠EBF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
【答案】①②③④
【解析】分析:①根据正方形的性质得AB=AD=DC,∠BAD=∠D=90°,又EA=DF,根据“SAS”可判断△ABE≌△DAF,②利用∠FAD+∠FAB=90°得到∠ABE+∠FAB=90°,则AE⊥BF;③利用APE∽△ADF可得![]() ,故可求解;④分别求出BE、AP、BP、PE的长,即可求解.
,故可求解;④分别求出BE、AP、BP、PE的长,即可求解.
详解: ∵四边形ABCD为正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
在△ABE和△DAF中
 ,
,
∴△ABE≌△DAF,故①正确;
∴∠ABE=∠FAD,
而∠FAD+∠FAB=90°,
∴∠ABE+∠FAB=90°,
∴∠APB=90°,
∴AF⊥BE,所以②正确;
由①得∠AEB=∠DFA
∴APE∽△ADF
∴![]()
∴![]()
∴![]() ,故③正确;
,故③正确;
连接BF,如图:

∵![]()
∴在Rt△ABE中,BE=![]()
∴AP= ,
,![]()
∴FP=![]()
∴tan∠EBF=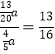 ,故④正确.
,故④正确.
故答案为:①②③④.

【题目】为了迎接浙江省中小学生健康体质测试,某学校开展“健康校园,阳光跳绳”活动,为此学校准备购置A,B,C三种跳绳.已知某厂家的跳绳的规格与价格如下表:
A绳子 | B绳子 | C绳子 | |
长度(米) | 8 | 6 | 4 |
单价(元/条) | 12 | 8 | 6 |
(1)已知购买A,B两种绳子共20条花了180元,问A,B两种绳子各购买了多少条?
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
(3)若该厂家有一根长200米的绳子,现将其裁成A,B,C三种绳子共40条(没有剩余)销售给学校,学校要求A种绳子的数量少于B种绳子的数量但不少于B种绳子的数量的一半,请直接写出所有的裁剪方案.