题目内容
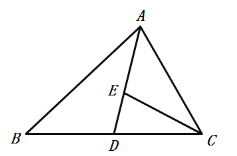
【题目】如图,已知在![]() 中,AD是
中,AD是![]() 的中线,∠DAC=∠B,点E在边AD上,CE=CD.
的中线,∠DAC=∠B,点E在边AD上,CE=CD.
(1)求证:![]() ;
;
(2)求证:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由CE=CD=BD转化比例式,再证出△ACE∽△BAD即可;
(2)由(1)中相似可得出,DC2=ADAE①,再证△ACD∽△BCA,得出AC2=BC·CD=2CD2②,结合①②即可得出结果.
证明:(1)∵AD为△ABC的中线,
∴BD=CD,
∵CD=CE,
∴BD=CD=CE,
∴∠CDE=∠CED,
∵∠CDE=∠B+∠BAD,∠CED=∠DAC+∠ACE,∠DAC=∠B,
∴∠BAD=∠ACE
∵△ACE∽△BAD,
∴![]()
∴![]() ;
;
(2)∵△ACE∽△BAD,
∴![]() ,
,
∴BDCE=AEAD,
∴DC2=ADAE①.
∵∠DAC=∠B,∠ACD=∠ACB,
∴△ACD∽△BCA,
∴![]()
∴AC2=BC·CD=2CD2②,
∴由①②可得,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目