题目内容
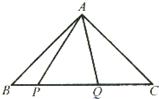 3、如图,△ABC中,∠BAC=90°,AB=AC,P、Q是BC上两点,且满足BP2+CQ2=PQ2,则∠PAQ的度数是
3、如图,△ABC中,∠BAC=90°,AB=AC,P、Q是BC上两点,且满足BP2+CQ2=PQ2,则∠PAQ的度数是45
°.分析:由∠BAC=90°,AB=AC,可将△AQC逆时针绕点A旋转90°得△ADB,AC与AB重合,连DP,根据旋转的性质得到∠1=∠C,AD=AQ,BD=CQ,∠DAQ=90°,则∠C=∠ABC=∠1=45°,得到∠DBP=2∠C=90°,根据勾股定理和BP2+CQ2=PQ2,得到DP=PQ,则有△ADP≌△AQP,得到∠DAP=∠PAQ,而∠DAQ=90°,即可求出∠PAQ的度数.
解答:解:如图,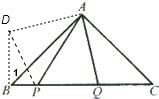 ∵∠BAC=90°,AB=AC,
∵∠BAC=90°,AB=AC,
∴将△AQC逆时针绕点A旋转90°得△ADB,AC与AB重合,连DP,
∴∠1=∠C,AD=AQ,BD=CQ,∠DAQ=90°,
而∠BAC=90°,AB=AC,
∴∠C=∠ABC=∠1=45°,
∴∠DBP=2∠C=90°,
∴DP2=DB2+BP2,
而QC2+BP2=PQ2,
∴DP=PQ
∴△ADP≌△AQP,
∴∠DAP=∠PAQ,
而∠DAQ=90°,
∴∠PAQ=45°.
故答案为45.
 ∵∠BAC=90°,AB=AC,
∵∠BAC=90°,AB=AC,∴将△AQC逆时针绕点A旋转90°得△ADB,AC与AB重合,连DP,
∴∠1=∠C,AD=AQ,BD=CQ,∠DAQ=90°,
而∠BAC=90°,AB=AC,
∴∠C=∠ABC=∠1=45°,
∴∠DBP=2∠C=90°,
∴DP2=DB2+BP2,
而QC2+BP2=PQ2,
∴DP=PQ
∴△ADP≌△AQP,
∴∠DAP=∠PAQ,
而∠DAQ=90°,
∴∠PAQ=45°.
故答案为45.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等腰直角三角形的性质和勾股定理以及三角形全等的判定与性质.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.