题目内容
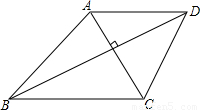
 如图,四边形的对角线AC、BD互相垂直,AC+BD=10,当AC、BD的长是多少时,四边形ABCD的面积最大?
如图,四边形的对角线AC、BD互相垂直,AC+BD=10,当AC、BD的长是多少时,四边形ABCD的面积最大?分析:根据已知设四边形ABCD面积为S,AC为x,则BD=10-x,进而求出S=-
x2+5x,再求出最值即可.
| 1 |
| 2 |
解答:解:设AC=x,四边形ABCD面积为S,则BD=10-x,
S=
x(10-x)=-
x2+5x,
∵-
<0,
∴抛物线开口向下,
当x=-
=5时,S最大=-
×52+5×5=
,
即当AC=5,BD=5时,四边形ABCD面积最大,最大值为
.
S=
| 1 |
| 2 |
| 1 |
| 2 |
∵-
| 1 |
| 2 |
∴抛物线开口向下,
当x=-
| 5 | ||
2×(-
|
| 1 |
| 2 |
| 25 |
| 2 |
即当AC=5,BD=5时,四边形ABCD面积最大,最大值为
| 25 |
| 2 |
点评:此题主要考查了二次函数的应用,根据已知正确得出二次函数关系是解题关键.

练习册系列答案
相关题目
 如图,四边形的对角线AC、BD互相垂直,AC+BD=10,当AC、BD的长是多少时,四边形ABCD的面积最大?
如图,四边形的对角线AC、BD互相垂直,AC+BD=10,当AC、BD的长是多少时,四边形ABCD的面积最大?