题目内容
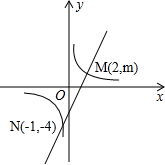
如图,一次函数y=ax+b与反比例函数y=
的图象交于M、N两点.
(1)求这两个函数的关系式;
(2)根据图象,写出使反比例函数值大于一次函数值时x的取值范围.
| k |
| x |
(1)求这两个函数的关系式;
(2)根据图象,写出使反比例函数值大于一次函数值时x的取值范围.

(1)把N(-1,-4)代入y=
得k=-1×(-4)=4,
所以反比例函数解析式为y=
;
把M(2,m)代入y=
得m=
,
解得m=2,
即M点坐标为(2,2),
把M(2,2)、N(-1,-4)代入y=ax+b得
,
解得
,
所以一次函数解析式为y=2x-2;
(2)当x<-1或0<x<2时,反比例函数值大于一次函数值.
| k |
| x |
所以反比例函数解析式为y=
| 4 |
| x |
把M(2,m)代入y=
| 4 |
| x |
| 4 |
| 2 |
解得m=2,
即M点坐标为(2,2),
把M(2,2)、N(-1,-4)代入y=ax+b得
|
解得
|
所以一次函数解析式为y=2x-2;
(2)当x<-1或0<x<2时,反比例函数值大于一次函数值.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
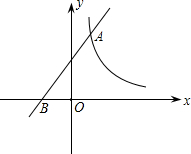

 相交于点A(1,3)、B(-3,n).
相交于点A(1,3)、B(-3,n).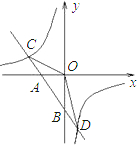 到线段OB.
到线段OB.