ЬтФПФкШн
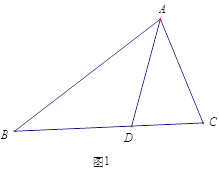
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуDЁЂEЗжБ№ЪЧЩфЯпABЁЂЩфЯпCBЩЯЕФЖЏЕуЃЌЕуDДгЕуAГіЗЂбиЩфЯпABвЦЖЏЃЌЕуEДгЕуBГіЗЂбиBGвЦЖЏЃЌЕуDЁЂЕуEЭЌЪБГіЗЂВЂЧвдЫЖЏЫйЖШЯрЭЌЃЎСЌНгCDЁЂDEЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕБЕуDвЦЖЏЕНЯпЖЮABЕФжаЕуЪБЃЌЧѓжЄЃКDE=DCЃЎ
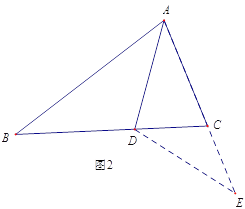
ЃЈ2ЃЉШчЭМЂкЃЌЕБЕуDдкЯпЖЮABЩЯвЦЖЏЕЋВЛЪЧжаЕуЪБЃЌЪдЬНЫїDEгыDCжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМЂлЃЌЕБЕуDвЦЖЏЕНЯпЖЮABЕФбгГЄЯпЩЯЃЌВЂЧвEDЁЭDCЪБЃЌЧѓЁЯDECЖШЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћЯъНтЃЛ
ЃЈ2ЃЉDE=DCЃЌРэгЩМћЯъНтЃЛ
ЃЈ3ЃЉЁЯDEC=45Ёу
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтПЩжЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌгЩЕШБпШ§НЧаЮМАжаЕуПЩжЊ
ЃЌгЩЕШБпШ§НЧаЮМАжаЕуПЩжЊ![]() ЃЌЖј
ЃЌЖј![]() ЃЌЫљвдПЩжЄ
ЃЌЫљвдПЩжЄ![]() ЃЌНјвЛВНПЩжЄ
ЃЌНјвЛВНПЩжЄ![]()
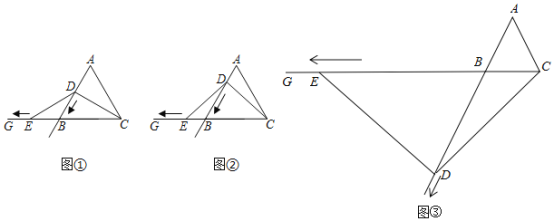
ЃЈ2ЃЉВТВт![]() ЃЌбАевЬѕМўжЄУїМДПЩ.зюГЃгУЕФЪЧжЄУїСНИіШ§НЧаЮШЋЕШЃЌЕЋЭМжаИјГіЕФШ§НЧаЮжаВЂЮДГіЯжШЋЕШШ§НЧаЮЃЌЫљвдЬэМгИЈжњЯпЃКдкЩфЯпABЩЯНиШЁ
ЃЌбАевЬѕМўжЄУїМДПЩ.зюГЃгУЕФЪЧжЄУїСНИіШ§НЧаЮШЋЕШЃЌЕЋЭМжаИјГіЕФШ§НЧаЮжаВЂЮДГіЯжШЋЕШШ§НЧаЮЃЌЫљвдЬэМгИЈжњЯпЃКдкЩфЯпABЩЯНиШЁ![]() ЃЌетбљжЛвЊжЄУї
ЃЌетбљжЛвЊжЄУї![]() МДПЩ.РћгУЕШБпШ§НЧаЮЕФаджЪМА
МДПЩ.РћгУЕШБпШ§НЧаЮЕФаджЪМА![]() ПЩжЊ
ПЩжЊ![]() ЮЊЕШБпШ§НЧаЮЃЌетбљЭЈЙ§СНИіЕШБпШ§НЧаЮМДПЩжЄУї
ЮЊЕШБпШ§НЧаЮЃЌетбљЭЈЙ§СНИіЕШБпШ§НЧаЮМДПЩжЄУї![]() .
.
ЃЈ3ЃЉАДееЕкЃЈ2ЃЉЮЪЕФЫМТЗЃЌзїГіРрЫЦЕФИЈжњЯпЃКдкЩфЯпCBЩЯНиШЁ![]() ЃЌгУЭЌбљЕФЗНЗЈжЄУї
ЃЌгУЭЌбљЕФЗНЗЈжЄУї![]() ЃЌгжвђЮЊEDЁЭDCЃЌЫљвд
ЃЌгжвђЮЊEDЁЭDCЃЌЫљвд![]() ЮЊЕШбќжЎМфШ§НЧаЮЃЌдђЁЯDECЖШЪ§ПЩЧѓ.
ЮЊЕШбќжЎМфШ§НЧаЮЃЌдђЁЯDECЖШЪ§ПЩЧѓ.
гЩЬтвтПЩжЊ![]()
ЁпDЮЊABЕФжаЕу
![]()
![]()
![]()
Ёп![]() ЮЊЕШБпШ§НЧаЮЃЌ
ЮЊЕШБпШ§НЧаЮЃЌ![]()
![]()
![]()
![]()
![]()
![]()
ЃЈ2ЃЉ![]()
РэгЩШчЯТЃК
дкЩфЯпABЩЯНиШЁ![]() ЃЌСЌНгEF
ЃЌСЌНгEF

Ёп![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ
![]()
![]()
Ёр![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ
![]()
гЩЬтвтжЊ![]()
![]()
![]()
МД![]()
![]()
![]()
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
![]()
![]()
ЃЈ3ЃЉШчЭМЃЌдкЩфЯпCBЩЯНиШЁ![]() ЃЌСЌНгDF
ЃЌСЌНгDF

Ёп![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ
![]()
![]()
Ёр![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ
![]()
![]()
гЩЬтвтжЊ![]()
![]()
![]()
МД![]()
![]()
![]()
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
![]()
![]()
ЁпEDЁЭDC
Ёр![]() ЮЊЕШбќжБНЧШ§НЧаЮ
ЮЊЕШбќжБНЧШ§НЧаЮ
![]()

 ЭЌВНСЗЯАКгФЯДѓбЇГіАцЩчЯЕСаД№АИ
ЭЌВНСЗЯАКгФЯДѓбЇГіАцЩчЯЕСаД№АИ ЭЌВНСЗЯАЮїФЯЪІЗЖДѓбЇГіАцЩчЯЕСаД№АИ
ЭЌВНСЗЯАЮїФЯЪІЗЖДѓбЇГіАцЩчЯЕСаД№АИ ВЙГфЯАЬтНЫеЯЕСаД№АИ
ВЙГфЯАЬтНЫеЯЕСаД№АИ