题目内容
已知:关于x的两个方程x2+(m+1)x+m-5=0…①与mx2+(n-1)x+m-4=0…②方程①有两个不相等的负实数根,方程②有两个实数根.(1)求证方程②的两根符号相同;
(2)设方程②的两根分别为α、β,若α:β=1:3,且n为整数,求m的最小整数值.
分析:(1)先由方程x2+(m+1)x+m-5=0有两个不相等的负实数根得出△>0,再根据根与系数的关系得出关于m的不等式组,求出m的取值范围,由方程②可知,当
≥0时此方程有两个同号实数根,再由①判断出
的符号即可;
(2)先根据α、β分别为方程mx2+(n-1)x+m-4=0的两个根,且α:β=1:3可得出α+β=4α=
,α=
,α•β=
=
,再由方程有两个实数根可得到△>0,与上式联立可得到关于m、n的方程组,求出m的取值范围,再与(1)中m的取值范围联立即可求出m的最小整数解.
| m-4 |
| m |
| m-4 |
| m |
(2)先根据α、β分别为方程mx2+(n-1)x+m-4=0的两个根,且α:β=1:3可得出α+β=4α=
| 1-n |
| m |
| 1-n |
| 4m |
| 3(1-n)2 |
| 16m2 |
| m-4 |
| m |
解答:解:(1)∵x2+(m+1)x+m-5=0,
∴△>0,即△=(m+2)2-4(m-5)=m2+2m+1-4m+20>0,
,
由②得m>-1由③得m>5,
∴m>5,
∴
>0,
∴方程②有两个同号实数根;
(2)∵α、β分别为方程mx2+(n-1)x+m-4=0的两个根,且α:β=1:3,
∴α+β=4α=
,α=
,
∴α•β=
=
,
∴
,
(n-1)2=
,4m2-16m≥0,
∴m≥4,
∵△=(n-1)2-4m(m-4)≥0,3α2=
.
∵
,
∴m的最小整数值为6.
∴△>0,即△=(m+2)2-4(m-5)=m2+2m+1-4m+20>0,
|
由②得m>-1由③得m>5,
∴m>5,
∴
| m-4 |
| m |
∴方程②有两个同号实数根;
(2)∵α、β分别为方程mx2+(n-1)x+m-4=0的两个根,且α:β=1:3,
∴α+β=4α=
| 1-n |
| m |
| 1-n |
| 4m |
∴α•β=
| 3(1-n)2 |
| 16m2 |
| m-4 |
| m |
∴
|
(n-1)2=
| 16m2-64m |
| 3 |
∴m≥4,
∵△=(n-1)2-4m(m-4)≥0,3α2=
| m-4 |
| m |
∵
|
∴m的最小整数值为6.
点评:本题考查的是一元二次方程根与系数的关系及根的判别式,有一定的难度,熟知根与系数的关系是解答此题的关键.

练习册系列答案
相关题目
探究发现:
解下列方程,将得到的解填入下面的表格中,观察表格中两个解的和与积,它们和原来的方程的系数有什么联系?
(1)x2-2x=0(2)x2+3x-4=0(3)x2-5x+6=0
| 方 程 | x1 | x2 | x1+x2 | x1•x2 |
| (1) | ||||
| (2) | ||||
| (3) |
(2)一般的,对于关于x的方程x2+px+q=0的两根为x1、x2,则x1+x2=______,x1•x2______.
(3)运用以上发现,解决下面的问题:
①已知一元二次方程x2-2x-7=0的两个根为x1,x2,则x1+x2的值为______
A.-2 B.2 C.-7 D.7
②已知x1,x2是方程x2-x-3=0的两根,试求(1+x1)(1+x2)和x12+x22的值.
解下列方程,将得到的解填入下面的表格中,观察表格中两个解的和与积,它们和原来的方程的系数有什么联系?
(1)x2-2x=0(2)x2+3x-4=0(3)x2-5x+6=0
| 方 程 | x1 | x2 | x1+x2 | x1.x2 |
| (1) | ______ | ______ | ______ | ______ |
| (2) | ______ | ______ | ______ | ______ |
| (3) | ______ | ______ | ______ | ______ |
一般的,对于关于x的方程x2+px+q=0(p,q为常数,p2-4q≥0)的两根为x1、x2
则x1+x2=______,x1.x2=______.
(2)运用以上发现,解决下面的问题:
①已知一元二次方程x2-2x-7=0的两个根为x1,x2,则x1+x2的值为______
A.-2 B.2 C.-7 D.7
②已知x1,x2是方程x2-x-3=0的两根,利用上述结论,不解方程,求x12+x22的值.
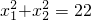 ,求m的值.
,求m的值.