题目内容
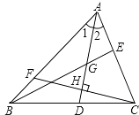
【题目】如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=62°,则∠AEB=_________.
【答案】152°.
【解析】
先求出∠ACE=∠BCD,再利用“边角边”证明△ACE和△BCD全等,根据全等三角形对应角相等可得∠CAE=∠CBD,从而求出∠CAE+∠CBE=∠EBD,再利用三角形的内角和等于180°列式求出∠EAB+∠EBA,然后再次利用三角形的内角和等于180°列式计算即可得解.
解:∵∠ACB=∠ECD=90°,
∴∠ACB∠BCE=∠ECD∠BCE,即∠ACE=∠BCD,
在△ACE和△BCD中,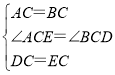 ,
,
∴△ACE≌△BCD,
∴∠CAE=∠CBD,
∴∠CAE+∠CBE=∠CBD+∠CBE=∠EBD=62°,
在△ABC中,∠EAB+∠EBA=180°(∠ACB+∠CAE+∠CBE)=180°(90°+62°)=28°,
在△ABE中,∠AEB=180°(∠EAB+∠EBA)=180°28°=152°,
故答案为:152°.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】甲、乙两名大学生竞选班长,现对甲、乙两名应聘者从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
应聘者 | 笔试 | 口试 | 得票 |
甲 | 85 | 83 | 90 |
乙 | 80 | 85 | 92 |
(1)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2:1:2来计算各人的成绩,那么又是谁会竞选上?