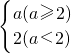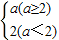题目内容
 阅读以下材料:
阅读以下材料:定义:对于三个数a、b、c,用max{a,b,c}表示这三个数中的最大数.
例如:①max{-1,2,3}=3; ②max{-1,2,a}=
|
根据以上材料,解决下列问题:
(1)如果max{2,2x+2,4-2x}=2x+2,求x的取值范围;
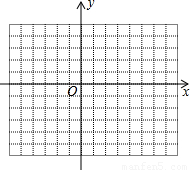
(2)在同一平面直角坐标系中分别作出函数y=x+1,y=(x-1)2,y=2-x的图象(不需列表),通过观察图象,填空:max{x+1,(x-1)2,2-x}的最小值为
| 3 |
| 2 |
| 3 |
| 2 |
分析:(1)根据材料提供的方法得到
解之即可求得x的取值范围;
(2)作出函数的图象后在坐标系中找到最低的即可确定最小值.
|
(2)作出函数的图象后在坐标系中找到最低的即可确定最小值.
解答:解:(1)由题意知
,
解之得x≥
,所以x的取值范围是x≥
;
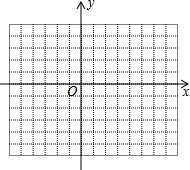
(2)函数图象如图所示
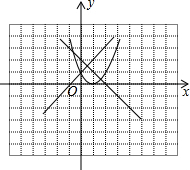
由图象可知:三个函数当x取相同的值时有最小值是
,
故max{ x+1,(x-1)2,2-x }的最小值为
.
|
解之得x≥
| 1 |
| 2 |
| 1 |
| 2 |
(2)函数图象如图所示

由图象可知:三个函数当x取相同的值时有最小值是
| 3 |
| 2 |
故max{ x+1,(x-1)2,2-x }的最小值为
| 3 |
| 2 |
点评:本题考查了二次函数及一次函数的图象,解题的关键是读懂题目提供的题目结合一次函数和二次函数的知识求解.

练习册系列答案
相关题目
 阅读以下材料:
阅读以下材料: