题目内容
【题目】如图![]() ,
, ![]() 平分
平分![]() ,
, ![]() 平分
平分![]() ,
, ![]() 和
和![]() 交于点
交于点![]() ,
, ![]() 为
为![]() 的中点,连结
的中点,连结![]() .
.
(![]() )找出图中所有的等腰三角形.
)找出图中所有的等腰三角形.
(![]() )若
)若![]() ,
, ![]() ,求
,求![]() 的长.
的长.
【答案】(![]() )所有的等腰三角形有:
)所有的等腰三角形有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;(
;(![]() )
)![]() .
.
【解析】试题分析:
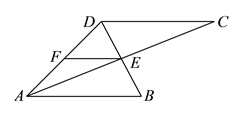
(1)由AB∥CD,AC平分∠BAD可得∠C=∠BAC=∠DAC,从而可得AD=CD,得到△ADC是等腰三角形;同理可△ABD是等腰三角形;证∠AED=90°,结合点F是AD中点,可得EF=FD=FA,从而可得△DEF和△AEF是等腰三角形;即图中共有4个等腰三角形;
(2)由∠AED=90°,AE=4,DE=3,由勾股定理可得AD=5,结合点F是AD中点,可得EF=![]() AD=2.5.
AD=2.5.
试题解析:
(![]() )图中等腰三角形共有4个,分别是:
)图中等腰三角形共有4个,分别是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .理由如下:
.理由如下:
∵AB∥CD,AC平分∠BAD,
∴∠C=∠BAC,∠BAC=∠DAC,
∴∠C=∠DAC,
∴AD=CD,
∴△ADC是等腰三角形;
同理可得:△ABD是等腰三角形;
∵BD平分∠ADC,AD=CD,
∴BD⊥AC,
∴∠AED=90°,
又∵点F是AD的中点,
∴EF=AF=DF,
∴△AEF和△DEF是等腰三角形;
综上所述,图中共有四个等腰三角形,分别是:△ADC、△ABD、△AEF和△DEF;

(![]() )∵∠AED=90°,AE=4,DE=3,
)∵∠AED=90°,AE=4,DE=3,
∴AD=![]() ,
,
又∵点F是AD的中点,
∴EF=![]() AD=
AD=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目