Question

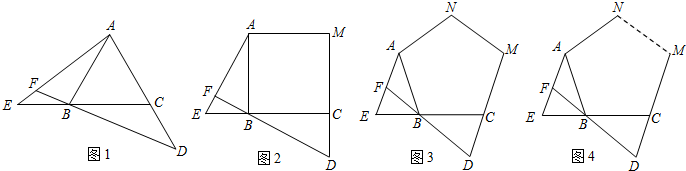
如图1所示，△ABC，△DEB为等边三角形，点E在线段DC上，AB与DC的交点为F，AE的延长线交BC于点G，AD=2DB

（1）求证：AD=CE；
（2）求证：AE⊥DC；
（3）以点E为坐标原点，DC、EA所在直线分别作x轴、y轴建立直角坐标系，如图2所示，且有A（0，3

3

），D（-3，0），设△ADF的面积为S₁，△ECG的面积为S₂，试判断式子S₂-S₁＞1是否成立？请说明理由．

Answer 1

分析：（1）根据等边三角形性质求出AB=BC，BD=BE，∠ABC=∠DBE=60°，求出∠ABD=∠CBE，根据SAS推出两三角形全等即可．
（2）取EC中点H，连接AH，求出EC=2BD=2DE，
即E、H为DC的三等份点，推出E为DH中点，求出DH=2DE=AD，得出△ADH是等边三角形，推出AD=AH，根据等腰三角形性质推出即可．
（3）过B作BI⊥DC于I，连接BH，证△ADE≌△HDB，推出∠DBH=∠AED=90°，BH=AE，求出DE=3，AE=3

3

，AD=2BD=2DE=6，求出IE=

1

2

DE=

3

2

，根据三角形面积公式得出S_△DBH=

1

2

×DH×BI=

1

2

×BD×BH，求出BI=

3

2

3

，求出C（6，0），求出直线AB的解析式是y=3

3

x+3

3

，直线BC的解析式是y=

3 3

5

x-

6 3

5

，求出F、G的坐标，根据三角形面积公式求出S₁，S₂，即可求出答案．

解答：证明：（1）∵△ABC，△DEB为等边三角形，
∴AB=BC，BD=BE，∠ABC=∠DBE=60°，
∴∠ABC-∠ABE=∠DBE-∠ABE，
∴∠ABD=∠CBE，
在△ABD和△CBE中

AB=BC ∠ABD=∠CBE BD=BE

∴△ABD≌△CBE（SAS），
∴AD=CE．

（2）证明：取EC中点H，连接AH，
∵△BDE是等边三角形，
∴∠EDB=∠DEB=60°，
∴∠BEC=180°-∠BED=120°，
由（1）知：△ADB≌△CEB，
∴∠ADB=∠BEC=120°，
∴∠ADE=120°-60°=60°，
∵AD=2BD，
∴EC=2BD=2DE，
即E、H为DC的三等份点，
∴E为DH中点，
∴DH=2DE=AD，
∵∠ADE=60°，
∴△ADH是等边三角形，
∴DH=AD=AH，
∴AE⊥DC（三线合一）．

（3）解：成立，
理由是：过B作BI⊥DC于I，连接BH，
∵在△ADE和△HDB中

AD=DH ∠ADE=∠HDB=60° DE=DB

∴△ADE≌△HDB（SAS），
∴∠DBH=∠AED=90°，BH=AE，
∵A（0，3

3

），D（-3，0），
∴DE=3，AE=3

3

，AD=2BD=2DE=6，
∵BD=BE，BI⊥CD，
∴IE=

1

2

DE=

3

2

，
∴S_△DBH=

1

2

×DH×BI=

1

2

×BD×BH，
即6×BI=3×3

3

，
BI=

3

2

3

，
由（1）知：EC=AD=6，
∴C（6，0），
设直线AB的解析式是y=kx+b，
把A（0，3

3

），B（-

3

2

，-

3

2

3

）代入得：

b=3 3 - 3 2 k+b=- 3 2 3

解得：k=3

3

，b=3

3

，
∴直线AB的解析式是y=3

3

x+3

3

，
当y=0时，x=-1，
即F（-1，0），
∴S1=S_△ADF=

1

2

DF×AE=

1

2

×2×3

3

=3

3

；
设直线BC的解析式是y=ax+c，
把C（6，0），B（-

3

2

，-

3

2

3

代入得：

6a+c=0 - 3 2 a+c=- 3 2 3

，
解得：a=

3 3

5

，c=-

6

5

3

，
即直线BC的解析式是y=

3 3

5

x-

6 3

5

，
当x=0时，y=-

6 3

5

，
即G（0，-

6 3

5

），
S₂=S_△ECG=

1

2

EG×EC=

1

2

×

6 3

5

×6=

18 3

5

，
∴S₂-S₁=

18 3

5

-3

3

=

3 3

5

，
∵3

3

=

27

，5=

25

，
∴

3 3

5

＞1，
即S₂-S₁＞1．

点评：本题考查了等边三角形的性质和判定，等腰三角形性质，用待定系数法求一次函数的解析式，三角形的面积，全等三角形的性质和判定的应用，难度偏大．