Question

如图，小明用一块有一个锐角为 30°的直角三角板测量树高，已知小明离树的距离为4米，DE为1．68米．
（1）这棵树大约有多高？（精确到0.01米）
（2）小明沿BE方向走1米，求此时小明看树顶C的仰角．（精确到1度）（参考数据tan37.6°≈0.77．）

Answer 1

分析：（1）根据题意得：AD=BE，CD=AD•sin∠CAD=AD•sin30°，又由DE为1.68米，即可求得棵树大约有多高；
（2）首先求得此时小明看树顶C的仰角的正切值，由tan37.6°≈0.77，即可求得此时小明看树顶C的仰角的度数．

解答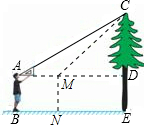：解：（1）根据题意得：AD=BE，
∴CD=AD•tan∠CAD=AD•tan30°=BE•tan30°=4×

3

3

≈2.31（米），
∴CE=DE+CD=1.68+2.31=3.99（米）．
∴这棵树大约有3.99米；

（2）根据题意得：AM=BN=1米，
∴DM=AD-AM=3米，
∴tan∠CMD=

CD

DM

=

2.31

3

≈0.77，
∴∠CMD=37.6°．
∴此时小明看树顶C的仰角约为37.6°．

点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．解此题的关键是掌握数形结合思想与方程思想的应用．