题目内容
有若干个数,第1个数记为a1,第2个数记为a2,第3个数记为a3,…,第n个数记为an,若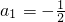 ,从第2个数起,每个数都等于l与它前面的那个数的差的倒数.
,从第2个数起,每个数都等于l与它前面的那个数的差的倒数.
(1)求a2,a3,a4的值;
(2)请你根据(1)的计算结果推断a2010的值,并写出推断过程.
解(1)a2= =
=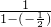 =
= ,a3=
,a3=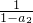 =
=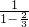 =3,a4=
=3,a4=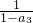 =
=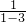 =-
=- ;
;
(2)由(1)这列数为- ,
, ,3,-
,3,- ,
, ,3,…,
,3,…,
而2010=3×670,
所以第2010个数为3,即a2010=3.
分析:(1)根据倒数的定义易得到a2= ,a3=3,a4=-
,a3=3,a4=- ;
;
(2)观察(1)的计算结果得到这列数为- ,
, ,3,-
,3,- ,
, ,3,…,每3个数一循环,由于而2010=3×870,则得到第2010个数为3.
,3,…,每3个数一循环,由于而2010=3×870,则得到第2010个数为3.
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
 =
=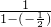 =
= ,a3=
,a3=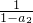 =
=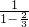 =3,a4=
=3,a4=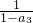 =
=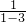 =-
=- ;
;(2)由(1)这列数为-
 ,
, ,3,-
,3,- ,
, ,3,…,
,3,…,而2010=3×670,
所以第2010个数为3,即a2010=3.
分析:(1)根据倒数的定义易得到a2=
 ,a3=3,a4=-
,a3=3,a4=- ;
;(2)观察(1)的计算结果得到这列数为-
 ,
, ,3,-
,3,- ,
, ,3,…,每3个数一循环,由于而2010=3×870,则得到第2010个数为3.
,3,…,每3个数一循环,由于而2010=3×870,则得到第2010个数为3.点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
 ,从第二个数起,每个数都等于1与前面那个数的差的倒数.
,从第二个数起,每个数都等于1与前面那个数的差的倒数. ,从第二个数起,每个数都等于1与前面那个数的差的倒数.
,从第二个数起,每个数都等于1与前面那个数的差的倒数. ,从第二个数起,每个数都等于1与前面那个数的差的倒数.
,从第二个数起,每个数都等于1与前面那个数的差的倒数.