题目内容
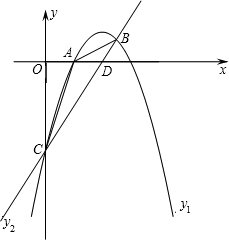
 如图,已知抛物线
如图,已知抛物线 的顶点坐标为(2,1),且经过点B(
的顶点坐标为(2,1),且经过点B( ),抛物线对称轴左侧与x轴交于点A,与y轴相交于点C.
),抛物线对称轴左侧与x轴交于点A,与y轴相交于点C.
(1)求抛物线解析式y1和直线BC的解析式y2;
(2)连接AB、AC,求△ABC的面积.
(3)根据图象直接写出y1<y2时自变量x的取值范围.
解:(1)∵抛物线的顶点坐标为(2,1),
∴y1=a(x-2)2+1,
∵抛物线经过点( ,
, ),
),
∴a( -2)2+1=
-2)2+1= ,
,
解得a=-1,
∴y1=-(x-2)2+1=-x2+4x-3,
当x=0,y=-3,
∴C(0,-3),
设直线BC解析式为y2=kx+b(k≠0),
则有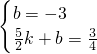 ,
,
解得 .
.
所以,直线BC的解析式为y2= x-3;
x-3;
(2)对于y1=-x2+4x-3,当y=0时,-x2+4x-3=0,
即x2-4x+3=0,
解得x1=1,x2=3,
∴点A的坐标为(1,0),
设直线BC与x轴相交于D,
对于y2= x-3,当y=0时,
x-3,当y=0时, x-3=0,
x-3=0,
解得x=2,
∴点D的坐标为(2,0),
∴AD=2-1=1,
则S△ABC=S△ABD+S△ACD,
= AD•|yB|+
AD•|yB|+ AD•|yC|=
AD•|yC|= ×1×
×1× +
+ ×1×3=
×1×3= ;
;
(3)由图得,当x<0或x> 时,y1<y2.
时,y1<y2.
分析:(1)设抛物线顶点式解析式y1=a(x-2)2+1,然后把点B的坐标代入求出a的值,即可求出抛物线解析式;令x=0求出点C的坐标,再设直线BC的解析式y2=kx+b(k≠0),利用待定系数法求一次函数解析式解答;
(2)令y=0,利用抛物线解析式求出点A的坐标,设直线BC与x轴的交点为D,利用直线BC的解析式求出点D的坐标,然后根据S△ABC=S△ABD+S△ACD,列式进行计算即可得解;
(3)根据图形,找出直线BC在抛物线上方部分的x的取值范围即可.
点评:本题是二次函数综合题型,主要考查了待定系数法求函数解析式(包括二次函数解析式、直线解析式),三角形的面积求解,利用函数图象解不等式,(1)利用顶点式解析式求解更加简便,(2)把△ABC分解成两个三角形求面积是解题的关键.
∴y1=a(x-2)2+1,
∵抛物线经过点(
 ,
, ),
),∴a(
 -2)2+1=
-2)2+1= ,
,解得a=-1,
∴y1=-(x-2)2+1=-x2+4x-3,
当x=0,y=-3,
∴C(0,-3),
设直线BC解析式为y2=kx+b(k≠0),
则有
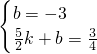 ,
,解得
 .
.
所以,直线BC的解析式为y2=
 x-3;
x-3;(2)对于y1=-x2+4x-3,当y=0时,-x2+4x-3=0,
即x2-4x+3=0,
解得x1=1,x2=3,
∴点A的坐标为(1,0),
设直线BC与x轴相交于D,
对于y2=
 x-3,当y=0时,
x-3,当y=0时, x-3=0,
x-3=0,解得x=2,
∴点D的坐标为(2,0),
∴AD=2-1=1,
则S△ABC=S△ABD+S△ACD,
=
 AD•|yB|+
AD•|yB|+ AD•|yC|=
AD•|yC|= ×1×
×1× +
+ ×1×3=
×1×3= ;
;(3)由图得,当x<0或x>
 时,y1<y2.
时,y1<y2.分析:(1)设抛物线顶点式解析式y1=a(x-2)2+1,然后把点B的坐标代入求出a的值,即可求出抛物线解析式;令x=0求出点C的坐标,再设直线BC的解析式y2=kx+b(k≠0),利用待定系数法求一次函数解析式解答;
(2)令y=0,利用抛物线解析式求出点A的坐标,设直线BC与x轴的交点为D,利用直线BC的解析式求出点D的坐标,然后根据S△ABC=S△ABD+S△ACD,列式进行计算即可得解;
(3)根据图形,找出直线BC在抛物线上方部分的x的取值范围即可.
点评:本题是二次函数综合题型,主要考查了待定系数法求函数解析式(包括二次函数解析式、直线解析式),三角形的面积求解,利用函数图象解不等式,(1)利用顶点式解析式求解更加简便,(2)把△ABC分解成两个三角形求面积是解题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
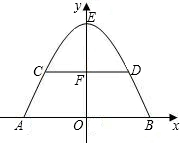
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系. 米,旗杆AB高为3米,C点的垂
米,旗杆AB高为3米,C点的垂 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系. 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.