题目内容
如图,已知AB是一条河,河的一边有两个村庄M和N,现要在河AB上修一个抽水站,请你在下图中作出抽水站的位置P,使点P到点M和点N的距离之和最短.(要求:用尺规作图,并写出已知、求作,保留作图痕迹,不写作法和结论)
已知:
求作:

【答案】分析:作点N关于直线AB的对称点N′,连接MN′交AB于点P,连接NP,由对称的性质可知N′P=NP,由两点之间线段最短可知点P即为所求点.
解答: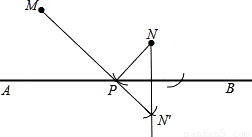 已知:直线AB及其同侧两点M、N.
已知:直线AB及其同侧两点M、N.
求作:直线AB上的点P,使点P到点M和点N的距离之和最短.
解:作点N关于直线AB的对称点N′,连接MN′交AB于点P,连接NP.
∵N、N′关于直线AB对称,
∴N′P=NP,
∴MP+NP=MP+N′P=MN′.
由两点之间线段最短可知,线段MN′的长即为MP+NP的最小值,故P点即为所求点.
点评:此题主要考查的是尺规作图和最短线路问题,熟知对称的性质及两点之间线段最短的知识是解答此题的关键,本题难度适中.
解答:
 已知:直线AB及其同侧两点M、N.
已知:直线AB及其同侧两点M、N.求作:直线AB上的点P,使点P到点M和点N的距离之和最短.
解:作点N关于直线AB的对称点N′,连接MN′交AB于点P,连接NP.
∵N、N′关于直线AB对称,
∴N′P=NP,
∴MP+NP=MP+N′P=MN′.
由两点之间线段最短可知,线段MN′的长即为MP+NP的最小值,故P点即为所求点.
点评:此题主要考查的是尺规作图和最短线路问题,熟知对称的性质及两点之间线段最短的知识是解答此题的关键,本题难度适中.

练习册系列答案
相关题目
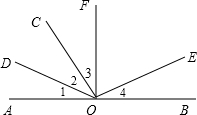
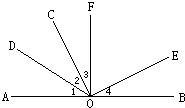 20、如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,OF⊥AB.则
20、如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,OF⊥AB.则 19、如图,已知AB是一条河,河的一边有两个村庄M和N,现要在河AB上修一个抽水站,请你在下图中作出抽水站的位置P,使点P到点M和点N的距离之和最短.
19、如图,已知AB是一条河,河的一边有两个村庄M和N,现要在河AB上修一个抽水站,请你在下图中作出抽水站的位置P,使点P到点M和点N的距离之和最短. 抽水站,请你在下图中作出抽水站的位置P,使点P到点M和点N的距离之和最短.
抽水站,请你在下图中作出抽水站的位置P,使点P到点M和点N的距离之和最短.