题目内容
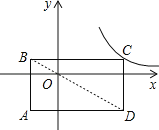
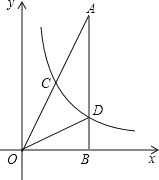
【题目】已知:如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
(1)求点A的坐标及该反比例函数的解析式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的解析式.

【答案】(1)A(1.5,2);y=![]() ;(2)y=﹣
;(2)y=﹣![]() x+3.
x+3.
【解析】
(1)根据线段的中点坐标的求法(线段中点的横纵坐标分别是线段2个端点的横纵坐标的和的一半)易得点A坐标,设出反比例函数的解析式,把A坐标代入即可;
(2)点B,D的横坐标相等,代入(1)中反比例函数的解析式中,求出点B的坐标,把A、B的坐标代入一次函数解析式,利用待定系数法求出函数解析式即可.
(1)过点A作AE⊥x轴于点E.
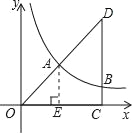
∵∠OCD=90°,
∴AE∥CD.A为OD中点,OC=3,DC=4,
∴AE是△OCD的中位线,
∴OE=EC=![]() OC,
OC,
∴A(1.5,2);
设反比例函数解析式为y=![]() (k≠0),
(k≠0),
那么k=1.5×2=3,
∴y=![]() ;
;
(2)当x=3时,y=1,
∴B(3,1);
设过A、B两点的直线的解析式为y=k2x+b,
则![]() ,
,
解得: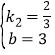 .
.
∴y=﹣![]() x+3.
x+3.

练习册系列答案
相关题目