题目内容
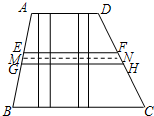 如图,梯形ABCD是世纪广场的示意图,上底AD=90m,下底BC=150m,高100m,虚线MN是梯形ABCD的中位线.要设计修建宽度相同的一条横向和两条纵向大理石通道,横向通道EGHF位于MN两旁,且EF、GH与MN之间的距离相等,两条纵向通道均与BC垂直,设通道宽度为xm.
如图,梯形ABCD是世纪广场的示意图,上底AD=90m,下底BC=150m,高100m,虚线MN是梯形ABCD的中位线.要设计修建宽度相同的一条横向和两条纵向大理石通道,横向通道EGHF位于MN两旁,且EF、GH与MN之间的距离相等,两条纵向通道均与BC垂直,设通道宽度为xm.
(1)试用含x的代数式表示横向通道EGHF的面积S1;
(2)用含x的代数式表示三条通道的面积和S2;
(3)若三条通道的面积和恰是梯形ABCD面积的 时,求通道宽度x.
时,求通道宽度x.
解:(1)∵上底AD=90m,下底BC=150m,
∴中位线的长度为:(90+150)÷2=120(m),
∴s1=120x;
(2)∵竖的通道的高是100m,宽是x,
∴两条竖的通道的面积是2×100x,
∵横的通道和两条竖的通道的公共部分的面是2x2,
∵横向通道面积是12x,
∴S2=120x+2×100x-2x2=320x-2x2;
(3)根据(2)可得:
120x+2×100x-2x2= ×
× ×(90+150)×100,
×(90+150)×100,
解得:x1=10,x2=150(不合题意,舍去),
则通道的宽是10m.
分析:(1)由于上底AD=90m,下底BC=150m,利用中位线的性质可以求出中位线的长度,然后利用梯形的面积公式即可求解;
(2)根据(1)求出的横向通道面积,再加上两条竖的通道,再减去公共部分,即可求出三条通道的面积和S2;
(3)根据由于三条通道的面积和恰好是梯形ABCD面积的 ,由此可以列出方程,求出符合题意的x即可.
,由此可以列出方程,求出符合题意的x即可.
点评:此题主要考查了一元二次方程的应用,解题时首先正确理解题意,然后根据题意列出方程,注意在求面积(2)时一定减去公共部分.
∴中位线的长度为:(90+150)÷2=120(m),
∴s1=120x;
(2)∵竖的通道的高是100m,宽是x,
∴两条竖的通道的面积是2×100x,
∵横的通道和两条竖的通道的公共部分的面是2x2,
∵横向通道面积是12x,
∴S2=120x+2×100x-2x2=320x-2x2;
(3)根据(2)可得:
120x+2×100x-2x2=
 ×
× ×(90+150)×100,
×(90+150)×100,解得:x1=10,x2=150(不合题意,舍去),
则通道的宽是10m.
分析:(1)由于上底AD=90m,下底BC=150m,利用中位线的性质可以求出中位线的长度,然后利用梯形的面积公式即可求解;
(2)根据(1)求出的横向通道面积,再加上两条竖的通道,再减去公共部分,即可求出三条通道的面积和S2;
(3)根据由于三条通道的面积和恰好是梯形ABCD面积的
 ,由此可以列出方程,求出符合题意的x即可.
,由此可以列出方程,求出符合题意的x即可.点评:此题主要考查了一元二次方程的应用,解题时首先正确理解题意,然后根据题意列出方程,注意在求面积(2)时一定减去公共部分.

练习册系列答案
相关题目
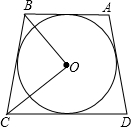 如图等腰梯形ABCD是⊙O的外切四边形,O是圆心,腰长4cm,则∠BOC=
如图等腰梯形ABCD是⊙O的外切四边形,O是圆心,腰长4cm,则∠BOC=
 (2012•凉山州)如图,梯形ABCD是直角梯形.
(2012•凉山州)如图,梯形ABCD是直角梯形. (2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.
(2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.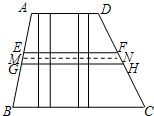 费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?
费用为0.05万元/m2,若设计要求通道宽度x≤8m,则宽度x为多少时,世纪广场修建总费用最少?最少费用为多少?