题目内容
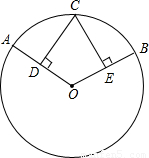
 如图,C是劣弧AB的中点,过点C分别作CD⊥OA,CE⊥OB,D、E分别是垂足,试判断CD、CE的大小关系,并证明你的结论.
如图,C是劣弧AB的中点,过点C分别作CD⊥OA,CE⊥OB,D、E分别是垂足,试判断CD、CE的大小关系,并证明你的结论.
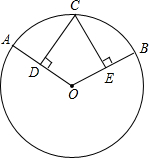
 解:CD=CE…(1分)
解:CD=CE…(1分)理由:连接CO.
∵C是弧AB的中点,∴
 =
= ,
,∴∠COD=∠COE…(2分),
∵CD⊥AO、CE⊥BO,∴∠CDO=∠CEO=90°…(3分),
又∵CO=CO…(4分),
∴△COD≌△COE…(5分),
∴CD=CE…(6分).
分析:连接CO.根据等弧所对的圆心角相等可以推知∠COD=∠COE,再由垂直的性质得到∠CDO=∠CEO=90°,所以由全等三角形的判定定理ASA证得△COD≌△COE;最后根据全等三角形的对应边相等推知CD=CE.
点评:本题考查了圆心角、弧、弦的关系,全等三角形的判定.在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等;圆心角、弧、弦的不等量关系:在同圆或等圆中,圆心角不等,所对的弧、弦、弦的弦心距不等,圆心角的所对的弧大,所对的弦大,所对的弦的弦心距反而小.需注意的是“在同圆或等圆中”的前提条件不能丢.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目

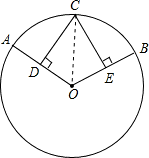
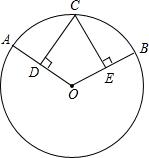 如图,C是劣弧AB的中点,过点C分别作CD⊥OA,CE⊥OB,D、E分别是垂足,试判断CD、CE的大小关系,并证明你的结论.
如图,C是劣弧AB的中点,过点C分别作CD⊥OA,CE⊥OB,D、E分别是垂足,试判断CD、CE的大小关系,并证明你的结论.