Question

【题目】如图1，在平面直角坐标系xOy中，直线l：y＝经过点A（4m，4），与y轴交于点B，抛物线经过点A，交y轴于点C．

⑴ 求直线l的解析式及抛物线的解析式；

⑵ 如图2，点D是直线l在第一象限内的一点，过点D作直线EF∥y轴，交抛物线于点E，交x轴于点F，连接AF，若∠CEF＝∠CBA，求AF的长；

⑶ 在（2）的结论下，若点P是直线EF上一点，点Q是直线l上一点．当△PFA与△QPA全等时，直接写出点P和相应的点Q的坐标.

Answer 1

【答案】(1) ;(2)5;(3)见解析.

【解析】分析：(1)把点A代入直线l解析式中，求出m，进而求出点A坐标，再代入抛物线解析式中，即可得出结论;(2)先判断出四边形CBDE是平行四边形，然后求出a,再得出点F坐标，最后由勾股定理得出结论；(3)分两种情况，利用全等三角形的对应边相等，建立方程求解，然后求出结论.

详解：⑴由直线l：y=经过点A（4m，4）

得：，解得：m=1

∴ 直线l的解析式为：y=

点A的坐标为（4，4）

∵ 抛物线经过点A

∴ 解得：b=1

∴ 抛物线的解析式为：

⑵如图1，过点A作AG⊥x轴，垂足为点G.

由点D是直线y=上的点，设点D的坐标为（4a，3a＋1）

∵ EF∥y轴

∴ 点E、F的横坐标为4a，∠CEF＋∠ECB=180°

∵ ∠CBA=∠CEF ∴ ∠CBA＋∠ECB=180°

∴ CE∥BD

∴ 四边形CBDE是平行四边形

∴ ED=BC

由BC=得：ED=3

将x=4a代入得：

∴

解得： ,

∴ 点F（1，0）

∴ GF=4－1=3

△AFG中，∠AGF=90°，AG=4

∴ .

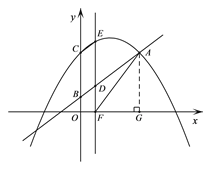
图1

⑶ 如图2，当点P（1，7）时，点Q（8，7）；

如图3，当点P（1，1）时，点Q（0，1）；

如图4，当点P（1，）时，点Q（，）；

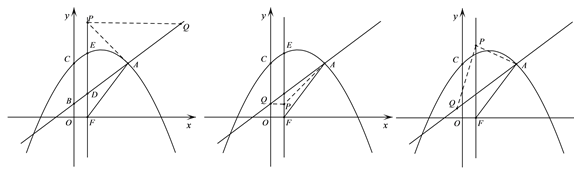
图2 图3 图4