题目内容
【题目】已知△ABC是等边三角形，D是BC边上的一个动点（点D不与B，C重合）△ADF是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．
（1）如图1，求证：△AFB≌△ADC； 
（2）请判断图1中四边形BCEF的形状，并说明理由；
（3）若D点在BC 边的延长线上，如图2，其它条件不变，请问（2）中结论还成立吗？如果成立，请说明理由． 
【答案】
（1）证明：∵△ABC和△ADF都是等边三角形，
∴AF=AD，AB=AC，∠FAD=∠BAC=60°，
又∵∠FAB=∠FAD﹣∠BAD，∠DAC=∠BAC﹣∠BAD，
∴∠FAB=∠DAC，
在△AFB和△ADC中，
，
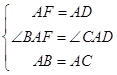∴△AFB≌△ADC（SAS）；
（2）解：由①得△AFB≌△ADC，
∴∠ABF=∠C=60°．
又∵∠BAC=∠C=60°，
∴∠ABF=∠BAC，
∴FB∥AC，
又∵BC∥EF，
∴四边形BCEF是平行四边形；
（3）解：成立，理由如下：
∵△ABC和△ADF都是等边三角形，
∴AF=AD，AB=AC，∠FAD=∠BAC=60°，
又∵∠FAB=∠BAC﹣∠FAE，∠DAC=∠FAD﹣∠FAE，
∴∠FAB=∠DAC，
在△AFB和△ADC中，
，
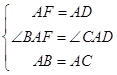∴△AFB≌△ADC（SAS）；
∴∠AFB=∠ADC．
又∵∠ADC+∠DAC=60°，∠EAF+∠DAC=60°，
∴∠ADC=∠EAF，
∴∠AFB=∠EAF，
∴BF∥AE，
又∵BC∥EF，
∴四边形BCEF是平行四边形．
【解析】（1）利用有两条边对应相等并且夹角相等的两个三角形全等即可证明△AFB≌△ADC；（2）四边形BCEF是平行四边形，因为△AFB≌△ADC，所以可得∠ABF=∠C=60°，进而证明∠ABF=∠BAC，则可得到FB∥AC，又BC∥EF，所以四边形BCEF是平行四边形；（3）易证AF=AD，AB=AC，∠FAD=∠BAC=60°，可得∠FAB=∠DAC，即可证明△AFB≌△ADC；根据△AFB≌△ADC可得∠ABF=∠ADC，进而求得∠AFB=∠EAF，求得BF∥AE，又BC∥EF，从而证得四边形BCEF是平行四边形．
【考点精析】根据题目的已知条件，利用平行四边形的判定的相关知识可以得到问题的答案，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．
