题目内容
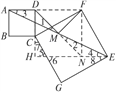
【题目】将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.

【答案】证明见解析
【解析】试题分析:根据观察它们的关系可能是MD=MF,MD⊥MF,证明思路:可以通过构建三角形来证明,延长DM交CE于点N,连接FD,FN,根据等腰直角三角形的性质,我们可以通过证明三角形DFN为等腰直角三角形,M为其斜边的中点来实现,那么要证明三角形DFN是个等腰直角三角形,且DM=MN,即要证明DF=FN,DM=MN, ∠DFN=90°,如果要证明DM=MN,那么可通过证明三角形ADM和MNE全等来实现,由于AD∥BE,那么∠1=∠2,M为AE中点,对顶角∠3=∠4,根据ASA可得出三角形ADM和MNE全等,那么可得出MN=DM,AD=NE,下一步证明三角形DCF和三角形FNE全等即可,由全等可得DF=FN, ∠5=∠6,根据同角的余角相等进行转化可证∠5+∠CFN=90°,那么我们可得出三角形DFN是个等腰直角三角形,且M是斜边DN的中点,因此可得出MD=MF, MD⊥MF.
试题解析:证法一:延长DM到N,使MN=MD,连接FD,FN,EN,延长EN与DC延长线交于点H.
∵MA=ME,∠1=∠2,MD=MN,
∴△AMD≌△EMN.
∴∠3=∠4,AD=NE.
又∵正方形ABCD、CGEF,
∴CF=EF,AD=DC,∠ADC=90°,
∠CFE=∠ADC=∠FEG=∠FCG=90°,
∴DC=NE,
∵∠3=∠4,∴AD∥EH.
∴∠H=∠ADC=90°,
∵∠G=90°,∠5=∠6,∴∠7=∠8,
∵∠7+∠DCF=∠8+∠FEN=90°,
∴∠DCF=∠FEN.
∵FC=FE,∴△DCF≌△NEF.
∴FD=FN,∠DFC=∠NFE.
∵∠CFE=90°,
∴∠DFN=90°.
∴FM⊥MD,MF=MD.
证法二:如右图,过点E作AD的平行线分别交DM、DC的延长线于N、H,连接DF、FN.
∴∠ADC=∠H,∠3=∠4.∵AM=ME,∠1=∠2,
∴△AMD≌△EMN.
∴DM=NM,AD=EN.
∵正方形ABCD、CGEF,
∴AD=DC,FC=FE,∠ADC=∠FCG=∠CFE=90°.
∴∠H=90°,∠5=∠NEF,DC=NE.
∴∠DCF+∠7=∠5+∠7=90°.
∴∠DCF=∠5=∠NEF.
∵FC=FE,∴△DCF≌△NEF.
∴FD=FN,∠DFC=∠NFE.∵∠CFE=90°,
∴∠DFN=90°.
∴FM⊥MD,MF=MD.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案