题目内容
【题目】数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图1可以解释完全平方公式(a+b)2=a2+2ab+b2 . 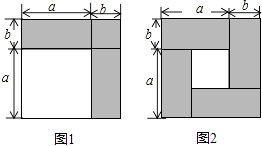
(1)如图2,请用不同的代数式表示图中阴影部分的面积,由此,你能得到怎样的等式?
(2)请说明这个等式成立;
(3)已知(2m+n)2=13,(2m﹣n)2=5,请利用上述等式求mn.
【答案】
(1)解:阴影部分的面积为:4ab或(a+b)2﹣(a﹣b)2,
得到等式:4ab=(a+b)2﹣(a﹣b)2
(2)解:右边=a2+2ab+b2﹣(a2﹣2ab+b2)=a2+2ab+b2﹣a2+2ab﹣b2=4ab=左边,即等式成立
(3)解:(2m+n)2﹣(2m﹣n)2=4×2mn,
13﹣5=8mn,
mn=1
【解析】(1)根据阴影部分的面积=4个小长方形的面积=大正方形的面积﹣小正方形的面积,利用完全平方公式,即可解答;(2)根据完全平方公式解答;(3)根据平方差公式解答.

练习册系列答案
相关题目