Question

20、两条直线上各有n个点，用这n对点按如下规则连接线段：
①同直线上的点不连接；
②连接的任意两条线段可以有共同的端点，但不得有其它的端点；
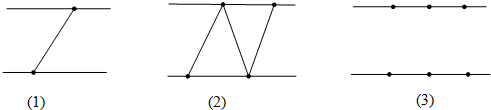
（1）画图说明当n=1、2、3时，连接的线段最多各有多少条？
（2）由（1）猜想n（n为正整数）对点之间连接的线段最多有多少条，证明你的结论．
（3）当n=2003时，所连接的线段最多有多少条？

Answer 1

分析：（1）根据题意，作图可得答案；
（2）分析可得，当n=1时的情况，此时图中线段最多的条数为1；当n=2时的一种情况，此时图中线段最多的条数为3；…故当有n对点时，设这n对点之间连接的直线段最多有P_n条，有P_n+1≥P_n+2．设对于n+1对点有另一种连法，有P_n+1-2≤P_n．由此，我们得到P_n+1=P_n+2，而P₁=1，P₂=3，所以P_n=1+2×（n-1）=2n-1．
（3）当n=2003时，代入（2）的结论即可求出所连接的线段最多的条数．

解答：解：（1）如图可以看出，n=1时，最多可以连接1条线段，n=2时，最多可以连接3条线段，n=3时，最多可以连接5条线段．

（2）猜想：对于正整数n，这n对点之间连接的直线段最多有2n-1条．
证明：将直线标记为l₁，l₂，它们上面的点从左到右排列为A₁，A₂A₃，┉，A_n和B₁，B₂，B₃，┉，B_n，设这n对点之间连接的直线段最多有P_n条，显然，其中必有A_nB_n这一条，否则，P_n就不是最多的数．
当在l₁，l₂分别加上笫n+1个点时，不妨设这两个点在A_n与B_n的右侧，那么除了原来已经有的P_n条直线段外，还可以连接A_n+1B_n，A_n+1B_n+1这两条线段，或连接A_nB_n+1，A_n+1B_n+1，这两条线段．
所以P_n+1≥P_n+2．
另一方面，设对于n+1对点有另一种连法：
考虑如图所示以A_n+1为端点的线段，若以A_n+1为端点的线段的条数大于1，则一定可以找到一个i≤n，使得对于任意的j＜i，A_n+1B_j都不在所画的线段中，这时，B_i+1，B_i+2，┉，B_n+1只能与A_n+1连接，不妨设A_n+1B_i+1，A_n+1B_i+2，┉，A_n+1B_n+1都已连接，此时图中的线段数为P_n+1，我们做如下操作：
去掉A_n+1B_i，连接A_nB_i+1，得到新的连接图，而新的连接图满足要求且线段总数不变，将此操作一直续断下去，直到与A_n+1连接的线段只有一条A_n+1B_n+1为止．最后图中，与点B_n+1相关的线段只剩两条，即A_nB_n+1，A_n+1B_n+1，去掉这两条线段，则剩余P_n+2-2条线段，而图形恰是n对点的连接图，所以P_n+1-2≤P_n．
由此，我们得到P_n+1=P_n+2，而P₁=1，P₂=3，所以P_n=1+2×（n-1）=2n-1．

（3）当n=2003时，P₂₀₀₃=4005（条）．

点评：此题考查了平面图形的有规律变化，要求学生的通过观察图形，分析、归纳并发现其中的规律，并应用规律解决问题．