题目内容
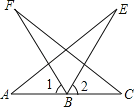
【题目】(1)如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
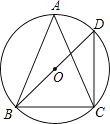
(2)如图,⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)利用∠1=∠2,即可得出∠ABE=∠CBF,再利用全等三角形的判定SAS得出即可.
(2)先根据圆周角定理可求出∠D=45°,∠BCD=90°,再根据三角形内角和定理可知△BCD是等腰直角三角形,由锐角三角函数的定义即可求出BC的长.
试题解析:(1)∵∠1=∠2,
∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF,
在△ABE与△CBF中,
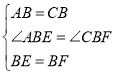 ,
,
∴△ABE≌△CBF(SAS).
(2)在⊙O中,∵∠A=45°,∠D=45°,
∵BD为⊙O的直径,
∴∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BC=BDsin45°,
∵BD=2,
∴BC=2×![]() =
=![]() .
.

练习册系列答案
相关题目
