题目内容
将一张边长分别为a,b(a>b)的矩形纸片ABCD折叠,使点C与点A重合,则折痕的长为
- A.
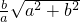
- B.
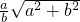
- C.
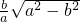
- D.
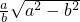
A
分析:由于A.C关于EF对称,那么AC⊥EF,于是∠AGE=90°,利用矩形的性质易证∠AGE=∠B,再结合∠GAE=∠BAC,易证△AGE∽△ABC,易求GE,再利用勾股定理可求AG,从而易求EF.
解答: 解:如图,设折痕EF与对角线AC的交点为G,则AC⊥EF,
解:如图,设折痕EF与对角线AC的交点为G,则AC⊥EF,
∵四边形ABCD是矩形,
∴∠B=90°,
又AC⊥EF,
∴∠AGE=90°,
∴∠AGE=∠B,
又∵∠GAE=∠BAC,
∴△AGE∽△ABC,
∴ ,
,
∴GE= ,
,
又∵AG= AC=
AC=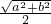 ,
,
∴EF=2GE=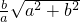 .
.
故选A.
点评:本题考查了矩形的性质、轴对称的性质、勾股定理、相似三角形的判定和性质.关键是理解对称点的连线垂直于折痕.
分析:由于A.C关于EF对称,那么AC⊥EF,于是∠AGE=90°,利用矩形的性质易证∠AGE=∠B,再结合∠GAE=∠BAC,易证△AGE∽△ABC,易求GE,再利用勾股定理可求AG,从而易求EF.
解答:
 解:如图,设折痕EF与对角线AC的交点为G,则AC⊥EF,
解:如图,设折痕EF与对角线AC的交点为G,则AC⊥EF,∵四边形ABCD是矩形,
∴∠B=90°,
又AC⊥EF,
∴∠AGE=90°,
∴∠AGE=∠B,
又∵∠GAE=∠BAC,
∴△AGE∽△ABC,
∴
 ,
,∴GE=
 ,
,又∵AG=
 AC=
AC=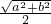 ,
,∴EF=2GE=
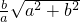 .
.故选A.
点评:本题考查了矩形的性质、轴对称的性质、勾股定理、相似三角形的判定和性质.关键是理解对称点的连线垂直于折痕.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
将一张边长分别为a,b(a>b)的矩形纸片ABCD折叠,使点C与点A重合,则折痕的长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|