题目内容

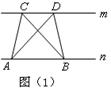
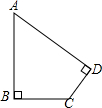如图，有一块土地的形状如图所示，∠B=∠D=90°，AB=20米，BC=15米，CD=7米，计算这块土地的面积．
分析：连接AC，则△ABC和△ACD均为直角三角形，根据AB，BC可以求出AC，根据AC，CD可以求出AD，根据直角三角形面积计算可以求出△ABC和△ACD的面积，四边形ABCD的面积为两个直角三角形面积之和．
解答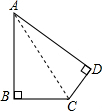：解：连接AC，将四边形分割成两个三角形，其面积为两个三角形的面积之和，
在直角△ABC中，AC为斜边，
则AC=
202+152
=25（米），
在直角△ACD中，AC为斜边
则AD=
252-72
=24（米），
四边形ABCD面积S=
1
2
AB×BC+
1
2
AD×CD=234（平方米）．
答：此块地的面积为234平方米．
点评：本题考查了勾股定理在实际生活中的应用以及直角三角形面积计算，本题中正确的运用勾股定理计算AC是解题的关键．
练习册系列答案
相关题目
23、阅读理解：如图（1），已知直线m∥n，A、B 为直线n上两点，C、D为直线m上两点，容易证明：△ABC的面积=△ABD的面积．
根据上述内容解决以下问题：已知正方形ABCD的边长为4，G是边CD上一点，以CG为边作正方形GCEF．
（1）如图（2），当点G与点D重合时，△BDF的面积为
8
．
（2）如图（3），当点G是CD的中点时，△BDF的面积为
8
．
（3）如图（4），当CG=a时，则△BDF的面积为
8
，并说明理由．
探索应用：小张家有一块正方形的土地如图（5），由于修建高速公路被占去一块三角形BCP区域．现决定在DP右侧补给小张一块土地，补偿后，土地变为四边形ABMD，要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上，请你在图中画出M点的位置，并简要叙述做法．

阅读理解：如图（1），已知直线m∥n，A、B 为直线n上两点，C、D为直线m上两点，容易证明：△ABC的面积=△ABD的面积．根据上述内容解决以下问题：

已知正方形ABCD的边长为4，G是边CD上一点，以CG为边作正方形GCEF．

（1）如图（2），当点G与点D重合时，△BDF的面积为      ；
（2）如图（3），当点G是CD的中点时，△BDF的面积为      ；
（3）如图（4），当CG = a时，则△BDF的面积为      ，并说明理由；
探索应用：小张家有一块正方形的土地如图（5），由于修建高速公路被占去一块三角形BCP区域．现决定在DP右侧补给小张一块土地，补偿后土地变为四边形ABMD，要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上，请你在图中画出M点的位置，并简要叙述做法．

阅读理解：如图（1），已知直线m∥n，A、B 为直线n上两点，C、D为直线m上两点，容易证明：△ABC的面积=△ABD的面积．根据上述内容解决以下问题：

已知正方形ABCD的边长为4，G是边CD上一点，以CG为边作正方形GCEF．

（1）如图（2），当点G与点D重合时，△BDF的面积为      ；

（2）如图（3），当点G是CD的中点时，△BDF的面积为      ；

（3）如图（4），当CG = a时，则△BDF的面积为      ，并说明理由；

探索应用：小张家有一块正方形的土地如图（5），由于修建高速公路被占去一块三角形BCP区域．现决定在DP右侧补给小张一块土地，补偿后土地变为四边形ABMD，要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上，请你在图中画出M点的位置，并简要叙述做法．

 
阅读理解：如图（1），已知直线m∥n，A、B 为直线n上两点，C、D为直线m上两点，容易证明：△ABC的面积=△ABD的面积．
根据上述内容解决以下问题：已知正方形ABCD的边长为4，G是边CD上一点，以CG为边作正方形GCEF．
（1）如图（2），当点G与点D重合时，△BDF的面积为______．
（2）如图（3），当点G是CD的中点时，△BDF的面积为______．
（3）如图（4），当CG=a时，则△BDF的面积为______，并说明理由．
探索应用：小张家有一块正方形的土地如图（5），由于修建高速公路被占去一块三角形BCP区域．现决定在DP右侧补给小张一块土地，补偿后，土地变为四边形ABMD，要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上，请你在图中画出M点的位置，并简要叙述作法．
阅读理解：如图（1），已知直线m∥n，A、B 为直线n上两点，C、D为直线m上两点，容易证明：△ABC的面积=△ABD的面积．
根据上述内容解决以下问题：已知正方形ABCD的边长为4，G是边CD上一点，以CG为边作正方形GCEF．
（1）如图（2），当点G与点D重合时，△BDF的面积为______．
（2）如图（3），当点G是CD的中点时，△BDF的面积为______．
（3）如图（4），当CG=a时，则△BDF的面积为______，并说明理由．
探索应用：小张家有一块正方形的土地如图（5），由于修建高速公路被占去一块三角形BCP区域．现决定在DP右侧补给小张一块土地，补偿后，土地变为四边形ABMD，要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上，请你在图中画出M点的位置，并简要叙述作法．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网