题目内容
【题目】如图, ![]() 平分
平分 ![]() ,
, ![]() 于点
于点 ![]() ,
, ![]() ,点 P
,点 P![]() 从
从 ![]() 出发,以
出发,以 ![]() 的速度沿线段
的速度沿线段 ![]() 向终点
向终点 ![]() 运动;同时,点
运动;同时,点 ![]() 从
从 ![]() 出发,以
出发,以 ![]() 的速度沿射线
的速度沿射线 ![]() 运动,当点 P到达终点
运动,当点 P到达终点 ![]() 时,则两点均停止运动. 那么经过
时,则两点均停止运动. 那么经过 ![]() ,能使
,能使 ![]() .
.
【答案】![]() 或
或 ![]()
![]()
【解析】解:(1)当P、Q移动到如图1所示位置时,过点A作AC![]() OM于点C,
OM于点C,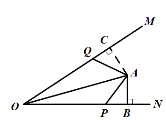
图1
设经过x秒时,AP=AQ,此时BP=x,OP=6-x,OQ=3x,
∵O A 平分 ∠ M O N ,∴AC=AB,又∵AP=AQ,∴![]() ACQ
ACQ![]()
![]() ABP,∴CQ=BP,
ABP,∴CQ=BP,
∵∠AOC=∠AOB,∠ACO=∠ABO,OA=OA,∴![]() ACO
ACO![]()
![]() ABO,∴CO=BO,
ABO,∴CO=BO,
∴CO-CQ=BO-BP,即OQ=OP,即:6-x=3x,解得:x=1.5.
(2)当P、Q移动到如图2所示位置时,过点A作AC![]() OM于点C,
OM于点C,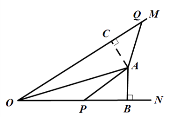
图2
设经过y秒时,AP=AQ,此时BP=y,OP=6-y,OQ=3y,
由(1)可得![]() ACQ
ACQ![]()
![]() ABP,∴CQ=BP=y,
ABP,∴CQ=BP=y,
由(1)可得![]() ACO
ACO![]()
![]() ABO,∴CO=BO,
ABO,∴CO=BO,
即:OQ-CQ=BO,即3y-y=6,解得:y=3.
(3)当点 P在(2)的基础上继续移动,到达终点 O 时,此过程无AP=AQ的情形.
所以答案是:1.5或3.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

练习册系列答案
相关题目

