题目内容
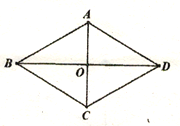
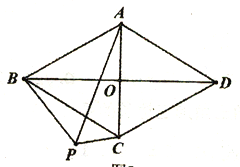
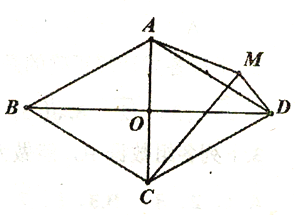
【题目】已知在菱形ABCD中,对角线AC、BD交于点O,AB=2AO;(1)如图1,求∠BAC的度数;(2)如图2,P为菱形ABCD外一点,连接AP、BP、CP,若∠CPB=120°,求证:CP+BP=AP;(3)如图3,M为菱形ABCD外一点,连接AM、CM、DM,若∠AMD=150°,
CM=2![]() ,DM=2,求四边形ACDM的面积。
,DM=2,求四边形ACDM的面积。
【答案】(1)∠BAC=60°;(2)见解析;(3)![]() .
.
【解析】
(1)如图1中,证明△ABC是等边三角形即可解决问题.
(2)在PA上截取PH,使得PH=PC,连接CH.证明△PCB≌△HCA(SAS)即可;
(3)如图3中,作AH⊥DM交DM的延长线于H,延长AC到N,使得CN=AC,连接DN.证明A,N,D,M四点共圆,外接圆的圆心是点C,推出AD=CM=![]() ,解直角三角形求出AH即可解决问题.
,解直角三角形求出AH即可解决问题.
解:(1)如图1中,
∵四边形ABCD是菱形,
∴AC⊥BD,∠ABD=∠CBD,
∴∠AOB=90°,
∵AB=2OA,
∴∠ABO=30°,
∴∠ABC=60°,
∵BA=BC,
∴△ABC是等边三角形,
∴∠BAC=60°;
(2)证明:如图2中,

在PA上截取PH,使得PH=PC,连接CH.
∵∠BPC=120°,∠BAC=60°,
∴∠BPC+∠BAC=180°,
∴A,B,P,C四点共圆,
∴∠APC=∠ABC=60°,
∵PH=PC,
∴△PCH是等边三角形,
∴PC=CH,∠PCH=∠ACB=60°,
∴∠PCB=∠HCA,
∵CB=CA,CP=CH,
∴△PCB≌△HCA(SAS),
∴PB=AH,
∴PA=PH+AH=PC+PB;
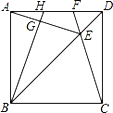
(3)解:如图3中,作AH⊥DM交DM的延长线于H,延长AC到N,使得CN=AC,连接DN.
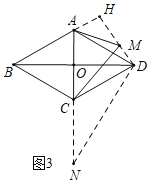
∵CA=CD=CN,
∴∠ADN=90°,
∵CD=CN,
∴∠N=∠CDN,
∵∠ACD=60°=∠N+∠CDN,
∴∠N=30°,
∵∠AMD=150°,
∴∠N+∠AMD=180°,
∴A,N,D,M四点共圆,外接圆的圆心是点C,
∴CA=CD=AD=CM=![]() ,
,
在Rt△AHM中,∵∠AMH=30°,
∴MH=![]() AH,设AH=x,则HM=
AH,设AH=x,则HM=![]() x,
x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴28=x2+(![]() x+2)2,
x+2)2,
解得x=![]() 或-2
或-2![]() (舍弃),
(舍弃),
∴AH=![]() ,
,
∴S四边形ACDM=S△ACD+S△ADM=![]() ×
×![]() +
+![]() ×2×
×2×![]() =
=![]() .
.

 名校课堂系列答案
名校课堂系列答案