题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 所在平面内一点,过点
所在平面内一点,过点![]() 分别作
分别作![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
若点![]() 在
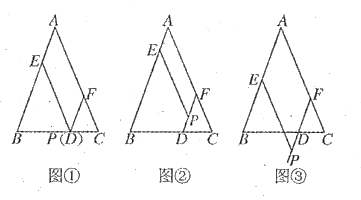
在![]() 上(如图①),此时
上(如图①),此时![]() ,可得结论:
,可得结论:![]() .
.
请应用上述信息解决下列问题:
当点![]() 分别在
分别在![]() 内(如图②),
内(如图②),![]() 外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,
外(如图③)时,上述结论是否成立?若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() ,与
,与![]() 之间又有怎样的数量关系,请写出你的猜想,不需要证明.
之间又有怎样的数量关系,请写出你的猜想,不需要证明.
【答案】当点![]() 在
在![]() 内时,成立,证明见解析;当点
内时,成立,证明见解析;当点![]() 在
在![]() 外时,不成立,数量关系为
外时,不成立,数量关系为![]() .
.
【解析】
当点![]() 在
在![]() 内时(如图②),通过FD∥AB与AB=AC可知,FD=FC.即PD+PF=FC.要想FC+PE=AB,根据等量代换,只需要知道PE=AF,PE=AF可通过证明四边形AEPF是平行四边形,用对边相等得到;
内时(如图②),通过FD∥AB与AB=AC可知,FD=FC.即PD+PF=FC.要想FC+PE=AB,根据等量代换,只需要知道PE=AF,PE=AF可通过证明四边形AEPF是平行四边形,用对边相等得到;
当点![]() 在
在![]() 外时(如图③),类似于①可知FD=FC;同样可通过证明四边形AEPF是平行四边形,得到对边PE=AF,此时FD=PF-PD,所以数量关系上类似于①但不同于①,只是FD=PF-PD的区别.
外时(如图③),类似于①可知FD=FC;同样可通过证明四边形AEPF是平行四边形,得到对边PE=AF,此时FD=PF-PD,所以数量关系上类似于①但不同于①,只是FD=PF-PD的区别.
解:当点![]() 在
在![]() 内时,上述结论
内时,上述结论![]() 成立.
成立.
证明:∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ;
;
当点![]() 在
在![]() 外时,上述结论不成立,此时数量关系为
外时,上述结论不成立,此时数量关系为![]() .
.
证明:∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
【题目】为了加强市民的节水意识,合理利用水资源,某市采用阶梯收费的调控手段以达到节水的目的,该市自来水收费价目表如下:
每月用水量 | 价格 | 注:水费按月结算,每户每月须缴纳5元污水处理费. |
不超出6m3的部分 | 2元/m3 | |
超出6m3不超出10m3的部分 | 3元/m3 | |
超出10m3的部分 | 5元/m3 |
若某户居民![]() 月份用水
月份用水![]() ,则应缴费
,则应缴费![]() (元),
(元),
(1)若用户![]() 月份共用水
月份共用水![]() ,则需缴费________;
,则需缴费________;
(2)若该户居民某月缴费![]() 元,则该户居民该月用水多少吨?
元,则该户居民该月用水多少吨?