Question

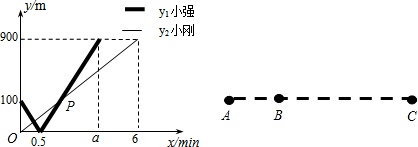
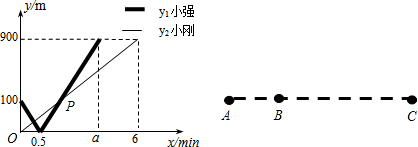
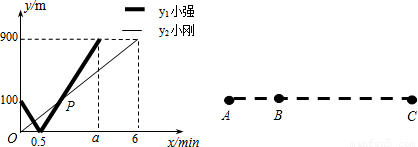
16、小刚和小强在一条由西向东的公路上行走，出发时间相同，小强从 A 出发，小刚从A往东的B处出发，两人到达C地后都停止．设两人行走x分钟后，小强、小刚离B的距离分别为y₁、y₂（m），y₁、y₂与x的函数关系如图所示：
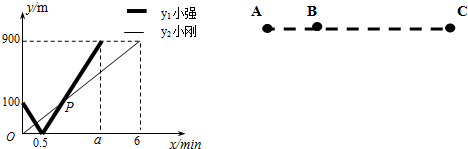
（1）根据图象可得：A、C两地间的距离为900m；a=

5

．
（2）求图中点P的坐标，并解释该点坐标所表示的实际意义；
（3）由于有雾，两人的距离不超过50m时才能够相互望见，求小强过了B地后至小刚到达C地前，小强可以望见小刚时x的取值范围．

Answer 1

分析：（1）根据图象可知小强的行走距离与时间是正比例函数关系，且经过（6，900），据此求出两地的距离；然后根据小刚行走100米用时0.5分钟求出速度，用路程除以速度即为时间；
（2）分别求得两图象的解析式，令y的值相等，求得x的值后，就求出了P点的坐标．
（3）当小强望见小刚时y₁-y₂≤50，据此求出t的取值范围即可．

解答：解：（1）有图象知：小强经过点（0，900），
即：小强用时6分钟行驶了900米到达C点，
∴A、C两地相距900米；
∵小刚用时0.5分钟行走了100米，
∴小刚的行走速度为：200米/秒，
∴900÷200=4.5，
∴a的值为4.5+0.5=5；

（2）∵直线y₁经过点（0.5，0）、（5，900），直线y₂经过点（0，0）、（6，900），
∴y₁=200t-100，y₂=150t，
∵y₁=y₂
∴200t-100=150t，
解得：t=2，
∴y₁=y₂=300
∴P点的坐标为（2，300）．
该点所表示的几何意义是小强第2分钟的时候正好追上小刚，此时距A点300米；

（3）当两人相互望见对方时：y₁-y₂≤50，
即：200t-100-150t≤50，
解得：t≤3，
∴小强望见小刚时的时间的取值范围是：t≤3．

点评：本题考查了一次函数的相关的知识，同时还考查了一元一次不等式的知识，是一道不错的一次函数综合题．