题目内容
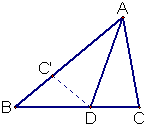 △ABC中,AD是∠BAC的平分线,且AB=AC+CD.若∠BAC=60°,则∠ABC的大小为( )
△ABC中,AD是∠BAC的平分线,且AB=AC+CD.若∠BAC=60°,则∠ABC的大小为( )分析:可在AB上取AC′=AC,则由题中条件可得BC′=C′D,即∠C=∠AC′D=2∠B,再由三角形的内角和即可求解∠B的大小.
解答:解:在AB上取AC′=AC,
∵AD是角平分线,
∴△ACD≌△AC′D,
又AB=AC+CD,得AB=AC′+C′D,故BC′=C′D,
∴∠C=∠AC'D=2∠B,
又∠B+∠C=180°-∠A=120°,
故∠B=40°.
选A.
∵AD是角平分线,
∴△ACD≌△AC′D,
又AB=AC+CD,得AB=AC′+C′D,故BC′=C′D,
∴∠C=∠AC'D=2∠B,
又∠B+∠C=180°-∠A=120°,
故∠B=40°.
选A.
点评:本题主要考查了全等三角形的判定及性质问题,能够掌握并熟练运用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
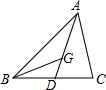 如图,在△ABC中,AD是中线,G是重心,
如图,在△ABC中,AD是中线,G是重心,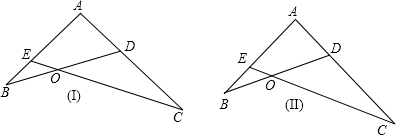
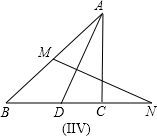
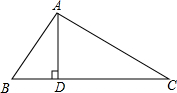 如图,在△ABC中,AD是BC边上的高,∠C=30°,AC=6,AB=4,求BD的长.(结果保留根号)
如图,在△ABC中,AD是BC边上的高,∠C=30°,AC=6,AB=4,求BD的长.(结果保留根号)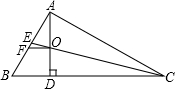 在直角△ABC中,AD是斜边上的高,角平分线CE交AD于O,过O引OF∥CB交AB于F.求证:AE=BF.
在直角△ABC中,AD是斜边上的高,角平分线CE交AD于O,过O引OF∥CB交AB于F.求证:AE=BF.